Learn to understand and determine prime numbers
Foreword
A method to determine prime numbers is known since at least the third century B.C.: It is a sieve named after Eratosthenes. The algorithm of this sieve can not be honored enough: It can be used as a basis for further discoveries in the research of primes. An important tool for this, set theory, is available thanks to its founder Georg Cantor.
But apart from the sieve of Eratosthenes, what else has been found in this area so far?
Mersenne prime
Fermat prime
Gaussian primes
Goldbach’s conjectures:
Every even number larger than 2 is the sum oft two prime numbers.
Every uneven number larger than 5 is the sum oft three prime numbers.
Euler’s formular n² + n + 41 gives prime numbers for every 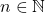 within the range 0 ≤ n ≤ 39. In case of n > 39 formular n² + n + 41 gives either a prime number or a compound number.
within the range 0 ≤ n ≤ 39. In case of n > 39 formular n² + n + 41 gives either a prime number or a compound number.
Theorems of Euclid, Fermat, Euler and Wilson
Prime number theorem
The Riemann hypothesis
Fermat primality test
Lucas-Lehmer test
Miller-Rabin primality test
AKS primality test
And others.
This prime number series shall show further ways to determine prime numbers.
One way is sketched in the above set diagram. It represents the relation of the three infinite sets  ,
, 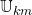 and the base set
and the base set 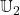 in a finite domain.
in a finite domain.
 represents the infinite set of all prime numbers.
represents the infinite set of all prime numbers.
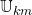 represents the infinite set of all composite uneven numbers.
represents the infinite set of all composite uneven numbers.
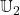 represents the infinite set of all uneven numbers greater than 2 and the number 2.
represents the infinite set of all uneven numbers greater than 2 and the number 2.
Any composite uneven number is the product of at least two uneven numbers, each greater than 2.
No element of  is element of
is element of 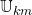 .
.
No element of 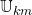 is element of
is element of  .
.
All elements of  are elements of base set
are elements of base set 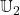 .
.
All elements of 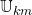 are also elements of base set
are also elements of base set 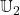 .
.
Base set 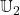 posseses no further elements beyond that.
posseses no further elements beyond that.
This means:  is the complementary set of
is the complementary set of 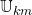 regarding base set
regarding base set 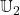 .
.
I.e.  can be determined explicitly, if
can be determined explicitly, if 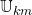 and base set
and base set 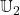 are known. Concerning this it will be entered detailed with proofs and examples in the entry
are known. Concerning this it will be entered detailed with proofs and examples in the entry
>The determination of all prime numbers in a selected range with the u-method<
Munich, 9 August 2019
Gottfried Färberböck


