Primzahlen verstehen und bestimmen lernen
Vorwort
Eine mindestens seit dem 3. Jahrhundert v. Chr. bekannte Methode zur Bestimmung aller Primzahlen bis zu einem gewählten Wert ist ein Sieb, der nach Eratosthenes benannt wurde. Der Algorithmus dieses Siebes kann nicht genug gewürdigt werden: Er kann als Fundament für weitere Erkenntnisse in der Primzahlenforschung verwendet werden. Ein wichtiges Werkzeug hierzu, die Mengenlehre, steht dank ihrem Begründer Georg Cantor, zur Verfügung.
Doch was wurde außer dem Sieb des Eratosthenes auf diesem Gebiet bisher noch gefunden?
Mersennesche Primzahlen
Fermatsche Primzahlen
Gaußsche Primzahlen
Goldbachsche Vermutungen:
Jede gerade Zahl > 2 ist Summe zweier Primzahlen.
Jede ungerade Zahl > 5 ist Summe dreier Primzahlen.
Euler’s Formel n² + n + 41 liefert mit 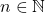 für jedes n im Bereich 0 ≤ n ≤ 39 Primzahlen. Für n > 39 ergibt n² + n + 41 entweder eine Primzahl oder eine zusammengesetzte Zahl.
für jedes n im Bereich 0 ≤ n ≤ 39 Primzahlen. Für n > 39 ergibt n² + n + 41 entweder eine Primzahl oder eine zusammengesetzte Zahl.
Willans Formel
Sätze von Euklid, Fermat, Euler und Wilson
Primzahlsatz
Riemannsche Vermutung
Fermat-Primzahltest
Lucas-Lehmer-Test
Rabin-Miller-Primzahltest
AKS-Primzahltest
Und anderes.
In dieser Primzahlenserie sollen weitere Wege aufgezeigt werden, wie Primzahlen bestimmt werden können.
Ein Weg ist in obigem Mengendiagramm skizziert. Das Diagramm stellt den Zusammenhang der drei unendlichen Mengen  ,
,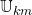 und der Grundmenge
und der Grundmenge 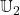 im endlichen Bereich dar.
im endlichen Bereich dar.
 steht für die unendliche Menge aller Primzahlen.
steht für die unendliche Menge aller Primzahlen.
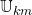 steht für die unendliche Menge aller zusammengesetzten, ungeraden Zahlen.
steht für die unendliche Menge aller zusammengesetzten, ungeraden Zahlen.
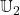 steht für die unendliche Menge aller ungeraden Zahlen größer 2 und der Zahl 2.
steht für die unendliche Menge aller ungeraden Zahlen größer 2 und der Zahl 2.
Eine zusammengesetzte, ungerade Zahl ist das Produkt von mindestens zwei ungeraden Zahlen, die jeweils größer als 2 sind.
Kein Element von  ist ein Element von
ist ein Element von 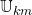 .
.
Kein Element von 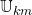 ist ein Element von
ist ein Element von  .
.
Alle Elemente von  sind auch Elemente von
sind auch Elemente von 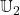 .
.
Alle Elemente von 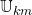 sind auch Elemente von
sind auch Elemente von 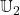 .
.
Darüber hinaus besitzt die Grundmenge 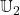 keine weiteren Elemente.
keine weiteren Elemente.
 ist also die Komplementärmenge von
ist also die Komplementärmenge von 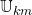 bezüglich der Grundmenge
bezüglich der Grundmenge 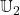 .
.
D.h.  kann explizit ermittelt werden, wenn
kann explizit ermittelt werden, wenn 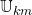 und die Grundmenge
und die Grundmenge 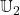 bekannt sind. Ausführlich mit Beweisen und Beispielen wird hierzu im Beitrag
bekannt sind. Ausführlich mit Beweisen und Beispielen wird hierzu im Beitrag
>Die Bestimmung aller Primzahlen in einem gewählten Bereich mit der u-Methode<
eingegangen.
München, 9. August 2019
Gottfried Färberböck


