Die duale Sinus-Primzahlfunktion
DIE PRIMZAHLENSERIE
Beitrag 12
Die duale Sinus-Primzahlfunktion
Die Primzahlfunktion ps(n) liefert für n ∈ ℕ immer eine Primzahl größer 2.
Die Primzahlfunktion ps(n) wird dual bezeichnet, weil sie
für vorhersagbare n ∈ ℕ immer die Primzahl 3 als Ergebnis hat
und
für die restlichen n ∈ ℕ alle Primzahlen größer 2 liefert.
Die duale Sinus-Primzahlfunktion lautet:
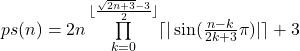
∧ n,k ∈ ℕ
Beweis:
Mit Hilfe der deterministischen Testfunktion ts(n) wird für ein gewähltes n das ts(n) ermittelt. Da ts(n) nur die Werte 0 für nicht prim und 1 für prim haben kann, gibt es für
ps(n)=2n*ts(n)+3
folgende Ergebnismöglichkeiten:
ts(n)=0 → ps(n)=3
ts(n)=1 → ps(n) ergibt eine Primzahl > 2.
Da
2n+3 für n ∈ ℕ
alle ungeraden Zahlen > 1 liefert und diese nur aus allen zusammengesetzten, ungeraden Zahlen und allen nicht zusammengesetzten, ungeraden Zahlen (= alle Primzahlen > 2) bestehen, müssen alle n, die in ts(n)=1 sind, in ps(n) alle Primzahlen > 2 sein.
Die vorhersagbaren n ∈ ℕ größer 0, die immer in der Funktion ps(n) die Primzahl 3 als Ergebnis haben, müssen natürlich der Formel
n=nkm = 2k²+6k+3+m(2k+3) ʌ k, m ∈ ℕ
entsprechen.
Was zu beweisen war.
München, 22. Januar 2023
Gottfried Färberböck


