Alle Primzahlen größer 2

DIE PRIMZAHLENSERIE

Beitrag 28

(Auch als Vortrag bei YouTube erhältlich)

Es sei bekannt, daß es unter den geraden Zahlen nur eine Primzahl gibt und zwar die 2. Bei den ungeraden Zahlen sieht es etwas anders aus: Die ungeraden Zahlen sind ein Gemisch von unendlich vielen Primzahlen und zusammengesetzten Zahlen.

Die Formel für alle ungeraden Zahlen größer 1 lautet

$2n+3$

wobei $n \in \mathbb{N}$ mit $n\ge 0$ .

Diese Formel liefert von n=0 bis n=2 ausschließlich Primzahlen:3,5,7.

Gemäß dem ungeraden Sieb ist die kleinste ungerade zusammengesetzte Zahl 3²=9. Ab n=3 liefert die Formel daher abwechselnd zusammengesetzte Zahlen und Primzahlen.

Ich habe die Formel 2n+3 mit einer Siebfaktorfunktion versehen, die gleichzeitig ein deterministischer Primzahltest ist. Das Ergebnis sieht so aus:

$3+2n\prod\limits_{k=0} ^{\frac{\sqrt{2n+3}-3}{2}} \lceil\sin^2(\frac{n-k}{2k+3}\pi)\rceil$

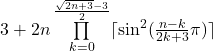
Diese Formel liefert von $n=0$ bis $n\rightarrow\infty$ ausschließlich Primzahlen und zwar alle größer 2.

Ist n=2k²+6k+3+m(2k+3) mit $k,m \in \mathbb{N}$ und $k,m\ge 0$ , dann hat die Siebfaktorfunktion immer den Wert 0 und liefert in diesem Falle immer die Primzahl 3 als Resultat. Für alle anderen $n \in \mathbb{N}$ liefert die Formel alle Primzahlen größer 2.

Als Menge dargestellt (die 3 taucht nur einmal auf), sind die ersten Primzahlen größer 2 bis 1000 gemäß obiger Formel:

{3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,

71,73,79,83,89,97,101,103,107,109,113,127,131,137,

139,149,151,157,163,167,173,179,181,191,193,197,

199,211,223,227,229,233,239,241,251,257,263,269,

271,277,281,283,293,307,311,313,317,331,337,347,

349,353,359,367,373,379,383,389,397,401,409,419,

421,431,433,439,443,449,457,461,463,467,479,487,

491,499,503,509,521,523,541,547,557,563,569,571,

577,587,593,599,601,607,613,617,619,631,641,643,

647,653,659,661,673,677,683,691,701,709,719,727,

733,739,743,751,757,761,769,773,787,797,809,811,

821,823,827,829,839,853,857,859,863,877,881,883,

887,907,911,919,929,937,941,947,953,967,971,977,

983,991,997}

München, 30. Mai 2024

Gottfried Färberböck

Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Alle Primzahlen größer 2