Alle Primzahlen in einem beliebigen Bereich mit dem ungeraden Sieb
DIE PRIMZAHLENSERIE
Beitrag 18
Alle Primzahlen in einem beliebigen Bereich mit dem ungeraden Sieb
- Man schreibe alle ungeraden Zahlen von
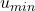 bis
bis 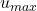 auf.
auf. - Man ziehe die Wurzel aus
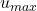 , notiere alle ungeraden Zahlen von 3 bis
, notiere alle ungeraden Zahlen von 3 bis 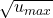 und wende den ungeraden Sieb auf diese Zahlenreihe an. Das Ergebnis sind alle Primfaktoren p, die für die Bestimmung aller Primzahlen P in der Zahlenreihe
und wende den ungeraden Sieb auf diese Zahlenreihe an. Das Ergebnis sind alle Primfaktoren p, die für die Bestimmung aller Primzahlen P in der Zahlenreihe 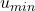 bis
bis 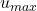 erforderlich sind.
erforderlich sind. - Man kennzeichne die 3 in der Liste mit den Primfaktoren p, ermittle den Rest aus der Division
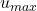 durch 3 und subtrahiere ihn von
durch 3 und subtrahiere ihn von 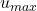 . Dadurch erhält man die erste, durch 3 teilbare Zahl. Ist diese gerade, wird 3 subtrahiert, sodaß man die erste ungerade, durch 3 teilbare Zahl erhält. Diese wird in der Liste
. Dadurch erhält man die erste, durch 3 teilbare Zahl. Ist diese gerade, wird 3 subtrahiert, sodaß man die erste ungerade, durch 3 teilbare Zahl erhält. Diese wird in der Liste 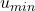 bis
bis 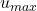 gestrichen und jede 3.te, kleinere Zahl.
gestrichen und jede 3.te, kleinere Zahl. - Man kennzeichne den nächsten Primfaktor p, ermittle den Rest aus der Division
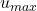 durch p und subtrahiere ihn von
durch p und subtrahiere ihn von 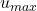 . Dadurch erhält man die erste, durch p teilbare Zahl. Ist diese gerade, wird p subtrahiert, sodaß man die erste ungerade, durch p teilbare Zahl erhält. Diese wird in der Liste
. Dadurch erhält man die erste, durch p teilbare Zahl. Ist diese gerade, wird p subtrahiert, sodaß man die erste ungerade, durch p teilbare Zahl erhält. Diese wird in der Liste 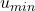 bis
bis 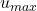 gestrichen und jede p.te, kleinere Zahl.
gestrichen und jede p.te, kleinere Zahl. - Schritt 4 wird für alle Primfaktoren p durchgeführt. Als Ergebnis erhält man alle Primzahlen P, die in der Liste
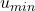 bis
bis 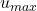 existieren sofern es überhaupt Primzahlen in dem gewählten Bereich
existieren sofern es überhaupt Primzahlen in dem gewählten Bereich 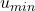 bis
bis 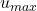 gibt.
gibt.
Beispiel: Alle Primzahlen in einem beliebigen Bereich mit dem ungeraden Sieb
München, 22. Oktober 2023
Gottfried Färberböck


