Über die tatsächliche Anzahl der Primzahlen (1)

DIE PRIMZAHLENSERIE

Beitrag 8

DIE PRIMZAHLFUNKTION $\pi(n_{max})$

Die Primzahlfunktion $\pi(n_{max})$ ist definiert als die Anzahl aller Primzahlen p, die nicht größer als $2n_{max}+3$ sind.

Die Primzahlfunktion $\pi(n_{max})$ liefert für $n_{max}$ ∈ ℕ die exakte Anzahl aller Primzahlen bis zu einem gewählten Wert $n_{max}$ . Es handelt sich also um keinen Näherungswert, sondern um die tatsächliche Anzahl:

$\pi(n_{max})=2+\sum\limits_{n=1}^{n_{max}}t(n)$

mit

$t(n)=\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

und

$k_{max}=\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}$

Eingesetzt ergibt dies

$\pi(n_{max})=2+\sum\limits_{n=1}^{n_{max}}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

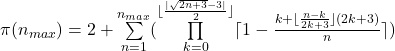
Legende:

$\sum\limits_{n=1}^{n_{max}}t(n)$ = Summe aller Ergebnisse von t(n) ab n=1 bis einschließlich dem gewählten $n_{max}$

Beweis:

Mit Hilfe der deterministischen Testfunktion t(n) wird für jedes n von n=1 bis zu einem gewählten $n_{max}$ t(n) ermittelt und dann zusammenaddiert. Da t(n) nur die Werte 0 für nicht prim und 1 für prim liefert, werden nur die Anzahl der Primzahlen von n=1 bis zu einem gewählten $n_{max}$ summiert. Da in t(n) für n nicht 0 gesetzt werden darf, wird 0 in 2n+3 eingesetzt:

2*0+3=3

Und bis zur Zahl 3 gibt es genau 2 Primzahlen: 2 und 3. Deswegen die 2 in der Funktion $\pi(n_{max})$ .

Was zu beweisen war.

München, 24. Oktober 2022

Gottfried Färberböck

Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Über die tatsächliche Anzahl der Primzahlen (1)