Rätsel über die Menge aller Primzahlen gelöst
DIE PRIMZAHLENSERIE
www.dieprimzahlenserie.com
Beitrag 16
Rätsel über die Menge aller Primzahlen gelöst
Es sei ![]() die Menge aller Primzahlen und p ∈
die Menge aller Primzahlen und p ∈ ![]() .
.
Mit der Mengenoperation
![]() \ {2} = {p | p =
\ {2} = {p | p = 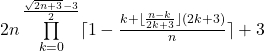 ʌ k ∈
ʌ k ∈ ![]() ʌ n ∈
ʌ n ∈ ![]() \ {0}}
\ {0}}
sind alle Primzahlen größer 2 bestimmbar.
Beweis: siehe Beitrag 9 DIE DUALE PRIMZAHLFUNKTION
Es gibt eine weitere Lösung für die Menge aller Primzahlen:
![]() \ {2} = {p | p =
\ {2} = {p | p = 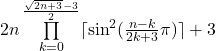 ʌ k,n ∈
ʌ k,n ∈ ![]() }
}
Beweis: siehe Beitrag 12 DIE DUALE SINUS-PRIMZAHLFUNKTION
22. März 2023 revidiert 11. Oktober 2024
Gottfried Färberböck


