Eine exakte Primzahlfunktion

DIE PRIMZAHLENSERIE

Beitrag 19

Die Primzahlfunktion $\pi(x)$ ist definiert als die Anzahl aller Primzahlen, die kleiner oder gleich der reellen Zahl x ist.

Seit mindestens 200 Jahren haben Mathematiker versucht, möglichst gute Näherungen an die Primzahlfunktion zu finden, angefangen bei Gauß über Legendre, Tschebyschow, Sylvester, Riemann u.a.

Mindestens eine exakte Primzahlfunktion, die ohne Näherungen auskommt und für jedes x kleiner oder gleich der reellen Zahl x immer die korrekte Anzahl der Primzahlen angibt, ist

$\pi(x})=2+\sum\limits_{n=1}^{\frac{x-3}{2}}(\prod\limits_{k=0} ^{{\frac{\sqrt{2n+3}-3} {2}}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

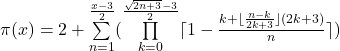
gültig für x ≥ 3 ∧ x $\in \mathbb{R}$

Nachfolgend ein Vergleich der Riemann-Näherungsformel R(x) mit meiner exakten Formel F(x) und der tatsächlichen Anzahl $\pi(x})$ :

x	$\pi(x)$	F(x)	R(x)	Riemann-Abweichung
100	25	25	26	1
1000	168	168	168	0
10000	1229	1229	1227	-2
100000	9592	9592	9587	-5
1000000	78498	78498	78527	29

Da für steigende x die Berechnungszeit immer länger wird, bzw. es interessant sein kann, wieviel Primzahlen in einem beliebigen Zahlenbereich sind, kann mit folgender Funktion gesplittet werden:

$\pi(x_{min},x_{max}})=\sum\limits_{\lceil\frac{x_{min}-3}{2}\rceil}^{\frac{x_{max}-3}{2}}(\prod\limits_{k=0} ^{{\frac{\sqrt{2n+3}-3} {2}}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

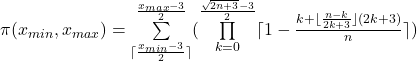
gültig für $x_{min},x_{max}$ ≥ 4 ∧ $x_{min},x_{max}$ $\in \mathbb{R}$

München, 5.April 2024

Gottfried Färberböck

Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Eine exakte Primzahlfunktion