Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Der x-Primzahltest

DIE PRIMZAHLENSERIE

Beitrag 20

Der x-Primzahltest

 

Setzt man in der gesplitteten Primzahlfunktion

\pi(x_{min},x_{max}})=\sum\limits_{\lceil\frac{x_{min}-3}{2}\rceil}^{\lfloor\frac{x_{max}-3}{2}\rfloor}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)

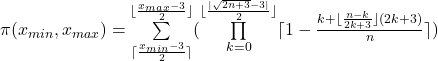
gültig für x_{min},x_{max} ≥ 4 ∧ x_{min},x_{max} \in \mathbb{R}

x_{min}=x_{max}=x}

ergibt sich der x-Primzahltest

t(x)=\sum\limits_{\lceil\frac{x-3}{2}\rceil}^{\lfloor\frac{x-3}{2}\rfloor}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)

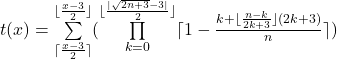
gültig für x ≥ 4 ∧ x \in \mathbb{R}

Da für steigende x die Berechnungszeit immer länger wird, kann mit folgender Funktion gesplittet werden:

t(x,k_{min},k_{max})=\sum\limits_{\lceil\frac{x-3}{2}\rceil}^{\lfloor\frac{x-3}{2}\rfloor}(\prod\limits_{k_{min}} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)

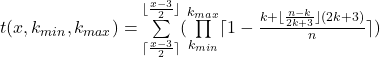
und

k_{max}={\lfloor{\frac{|\sqrt{x}-3|} {2}\rfloor}}

 

Beispiel: Es soll überprüft werden, ob 10^1000000+3 eine Primzahl ist. Diese Zahl hat eine Million Stellen plus eine weitere Stelle.

Für k_{min}=0 und k_{max}=1000 ergibt t(10^1000000+3)=0. D.h. 10^1000000+3 ist keine Primzahl.

 

München, 7.April 2024

Gottfried Färberböck