Die i-te Primzahl
DIE PRIMZAHLENSERIE
Beitrag 21
Die i-te Primzahl
Auf Hinweis eines Youtube-Users hin, habe ich mich mit der Willans Formel befaßt. Der Mathematiker Willans fand bereits 1964 eine Formel für die n-te Primzahl. Sie basiert auf einem Satz von Wilson. Laut Wikipedia ist sie nicht effizient. Nach eigener Überprüfung ist ab ca. der zehnten Primzahl bereits ein Hochleistungsrechner erforderlich.
In Anlehnung an die Willans Formel habe ich eine modifizierte Formel für die i-te Primzahl entwickelt. Sie basiert nicht auf dem Satz von Wilson, sondern auf eigenen Erkenntnissen. Obwohl meine Formel etwas effektiver ist als die Willans Formel, kann sie aber trotzdem nicht als effizient eingestuft werden, da bereits ab der 101-ten Primzahl die Rechenzeit relativ lang ist und verstärkt den Einsatz eines Hochleistungsrechners erforderlich macht.
Trotzdem nachfolgend die Formel:
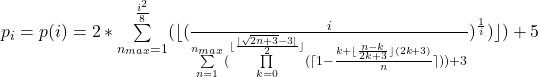
gültig für i ≥ 3 ∧ i ![]()
wobei
![]()
und
![]()
als bekannt vorausgesetzt werden.
Die Formel liefert dann alle weiteren Primzahlen in Reihenfolge mit
![]()
![]()
![]()
![]()
![]()
usw.
München, 11.April 2024
Gottfried Färberböck


