Die nächste Primzahl
DIE PRIMZAHLENSERIE
Beitrag 23
Die nächste Primzahl
Es sei U eine ungerade Zahl. Gesucht sei die nächste Primzahl.
Dies kann bewerkstelligt werden, indem zuerst die Anzahl der Primzahlen bis U und anschließend die erste, U folgende Primzahl ermittelt wird. Ich habe das Verfahren in zwei Schritte aufgeteilt, da Computer bei einem Schritt zu stark belastet würden.
![]() sei die Anzahl der Primzahlen bis einschließlich der ungeraden Zahl U. Dann gilt:
sei die Anzahl der Primzahlen bis einschließlich der ungeraden Zahl U. Dann gilt:
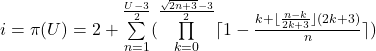
und
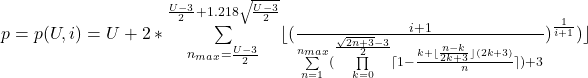
gültig für U ≥ 5 ∧ U ![]()
Beispiele:
Es sei U=5. Eingesetzt in die Formel für ![]() ergibt i=3. D.h. bis einschließlich der Zahl 5 gibt es drei Primzahlen. Und tatsächlich: Es sind die Primzahlen 2, 3 und 5. Damit kann die nächst folgende Primzahl p berechnet werden mit p(5,3)=7. Und 7 ist tatsächlich die erst größere Primzahl nach 5.
ergibt i=3. D.h. bis einschließlich der Zahl 5 gibt es drei Primzahlen. Und tatsächlich: Es sind die Primzahlen 2, 3 und 5. Damit kann die nächst folgende Primzahl p berechnet werden mit p(5,3)=7. Und 7 ist tatsächlich die erst größere Primzahl nach 5.
Es sei U=713. Eingesetzt in die Formel für ![]() ergibt i=127. D.h. bis einschließlich der Zahl 713 gibt es 127 Primzahlen. Damit kann p berechnet werden mit p(713,127)=719.
ergibt i=127. D.h. bis einschließlich der Zahl 713 gibt es 127 Primzahlen. Damit kann p berechnet werden mit p(713,127)=719.
Getestet mit meinem Primzahlentest
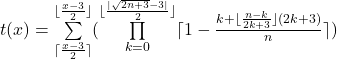
gültig für ![]() ≥ 4 ∧
≥ 4 ∧ ![]()
![]()
ergibt folgende Werte:
t(713)=0 d.h. 713 ist nicht prim
t(715)=0 d.h. 715 ist nicht prim
t(717)=0 d.h. 717 ist nicht prim
t(719)=1 d.h. 719 ist prim
Damit ist nachgewiesen, daß 719 die erste Primzahl ist, die der ungeraden Zahl 713 folgt.
München, 21. April 2024
Gottfried Färberböck


