Die Primzahlfunktion, der Primzahlsatz und die tatsächliche Anzahl der Primzahlen

DIE PRIMZAHLENSERIE

Beitrag 15

Die Primzahlfunktion $\pi(x)$ ist definiert als die Anzahl der Primzahlen p, die nicht größer als x sind:

$\pi(x)$ =|{ $p \in \mathbb{P}$ ∧ p ≤ x ∧ $x \in \mathbb{R}$ }|

Legende:

| $\mathbb{M}$ | = Mächtigkeit einer Menge $\mathbb{M}$

$\mathbb{P}$ = Menge der Primzahlen

$\mathbb{R}$ = Menge der reellen Zahlen

Gauß fand schon im Alter von 15 Jahren eine erste Näherung:

$\pi(x)$ ~ $\frac{x}{\ln {x}}$

gültig für x ≥ 3

Diese Näherung wurde als Grundlage für den Primzahlsatzsatz genommen, der folgendes aussagt:

$\lim\limits_ {x \to \infty$ $\frac{\pi(x)}{(\frac{x}{\ln {x}})}}$ =1

Später wurden noch bessere Näherungen gefunden.

Die Primzahlfunktion $\pi(n_{max})$ ist definiert als die Anzahl der Primzahlen p, die nicht größer als $2n_{max}+3$ sind:

$\pi(n_{max})=2+\sum\limits_{n=1}^{n_{max}}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

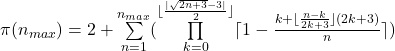
Die Primzahlfunktion $\pi(n_{max})$ liefert für $n_{max}$ ∈ ℕ die exakte Anzahl aller Primzahlen bis zu einem gewählten Wert $n_{max}$ . Es handelt sich also um keinen Näherungswert, sondern um die tatsächliche Anzahl.

Vergleich $\pi(x)$ ~ $\lfloor\frac{x}{\ln {x}}\rfloor$ mit der tatsächlichen Anzahl $\pi(n_{max})$ :

x	$n_{max}=\lfloor\frac{x-3}{2}\rfloor$	$\pi(x)$ ~ $\lfloor\frac{x}{\ln {x}}\rfloor$	Tatsächliche Anzahl $\pi(n_{max})$	Abweichung
10	3	4	4	0
100	48	21	25	4
1000	498	144	168	24
10000	4998	1085	1229	144
100000	49998	8685	9592	907
1000000	499998	72382	78498	6116

München, 11.März 2023

Gottfried Färberböck

Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Die Primzahlfunktion, der Primzahlsatz und die tatsächliche Anzahl der Primzahlen