Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Mathematiker-Traum: Alle Primzahlen nur mit ihrer Ordnungszahl berechnen

DIE PRIMZAHLENSERIE

Beitrag 22

Mathematiker-Traum:

Alle Primzahlen nur mit ihrer Ordnungszahl berechnen

 

Scheinbar gibt es keine Ordnung in der Unordnung der Primzahlen.

Doch der Schein trügt.

Die Primzahlen gehorchen u.a. folgender Ordnungsformel:

p_{i}=p(i)=2i-1+2*\sum\limits_{n_{max}=i-2}^{0,6i*ln(i)}}(\lfloor(\frac{i}{\sum\limits_{n=1}^{n_{max}}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} (\lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil))+3})^\frac{1}{i})\rfloor)

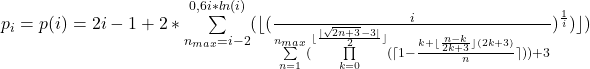
gültig für i > 1 ∧ i \in \mathbb{N}

wobei

p_{1}=2

als bekannt vorausgesetzt wird.

Die Formel liefert dann alle weiteren Primzahlen in Reihenfolge mit

p_{2}=3

p_{3}=5

p_{4}=7

p_{5}=11

p_{6}=13

p_{7}=17

…..

p_{60}=281

…..

p_{100}=541

…..

p_{200}=1223

usw.

Doch Achtung: Mit steigender Ordnungszahl kommt jeder Rechner und sogar jeder Hochleistungsrechner bzw. Supercomputer im Universum früher oder später an seine Grenzen!

 

München, 19.April 2024

Gottfried Färberböck