All prime numbers greater than 2

Let it known that there is only one prime number among the even numbers, namely 2. The situation is somewhat different for the odd numbers: The odd numbers are a mixture of infinitely many prime numbers and composite numbers.

The formula for all odd numbers greater than 1 is

where with .

This formula returns only prime numbers from n=0 to n=2: 3,5,7.

According to the odd sieve, the smallest odd composite number is 3²=9. From n=3, the formula therefore alternates between composite numbers and prime numbers.

I have added a sieve factor function to the formula 2n+3, which is also a deterministic prime number test. The result is:

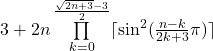
This formula provides from to exclusively prime numbers, all greater than 2.

If n=2k²+6k+3+m(2k+3) with and , then the sieve factor function always has the value 0 and in this case always returns the prime number 3 as the result. For all other the formula returns all prime numbers greater than 2.

Represented as a set (the 3 only appears once), the first prime numbers greater than 2 to 1000 are according to the above formula:

{3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,

71,73,79,83,89,97,101,103,107,109,113,127,131,137,

139,149,151,157,163,167,173,179,181,191,193,197,

199,211,223,227,229,233,239,241,251,257,263,269,

271,277,281,283,293,307,311,313,317,331,337,347,

349,353,359,367,373,379,383,389,397,401,409,419,

421,431,433,439,443,449,457,461,463,467,479,487,

491,499,503,509,521,523,541,547,557,563,569,571,

577,587,593,599,601,607,613,617,619,631,641,643,

647,653,659,661,673,677,683,691,701,709,719,727,

733,739,743,751,757,761,769,773,787,797,809,811,

821,823,827,829,839,853,857,859,863,877,881,883,

887,907,911,919,929,937,941,947,953,967,971,977,

983,991,997}

Munich, 30 May 2024

Gottfried Färberböck