Mystery about the set of all prime numbers solved
PRIME NUMBER SERIES 16
Mystery about the set of all prime numbers solved
With
![]() \ {2} = {p | p =
\ {2} = {p | p = 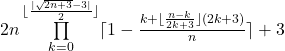 ʌ k ∈
ʌ k ∈ ![]() ʌ n ∈
ʌ n ∈ ![]() \ {0}}
\ {0}}
all prime numbers greater than 2 are given.
Proof: see PRIME NUMBER SERIES 9 THE DUAL PRIM NUMBER FUNCTION
There is another solution for the set of all prime numbers:
![]() \ {2} = {p | p =
\ {2} = {p | p = 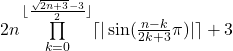 ʌ k,n ∈
ʌ k,n ∈ ![]() }
}
Proof: see PRIME NUMBER SERIES 12 THE DUAL SINE PRIME FUNCTION
Munich, March 22, 2023
Gottfried Färberböck


