One formula for all prime numbers

THE PRIME NUMBER SERIES 29

One formula for all prime numbers

One of the possible formulas for all prime numbers is

$p_{i}=p(i)=2*\lfloor0.56458i*ln(i)\rfloor-1+2*\sum\limits_{n_{max}=\lfloor0.56458i*ln(i)\rfloor-2}^{0.587i*ln(i)}}(\lfloor(\frac{i}{\sum\limits_{n=1}^{n_{max}}(\prod\limits_{k=0} ^{{\frac{\sqrt{2n+3}-3} {2}}} (\lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil))+3})^\frac{1}{i})\rfloor)$

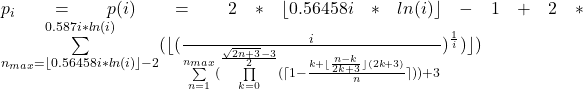
valid for i > 2 ∧ i $\in \mathbb{N}$

whereby

$p_{1}=2$

and

$p_{2}=3$

be presumed to be known.

The formula then returns ALL OTHER PRIME NUMBERS EXACTLY ORDERED ON THE NUMBER LINE with

$p_{3}=5$

$p_{4}=7$

$p_{5}=11$

$p_{6}=13$

$p_{7}=17$

$p_{8}=19$

$p_{9}=23$

$p_{10}=29$

$p_{11}=31$

$p_{12}=37$

$p_{13}=41$

$p_{14}=43$

$p_{15}=47$

$p_{16}=53$

$p_{17}=59$

and so on

$p_{60}=281$

and so on

$p_{100}$ = $541$

and so on

$p_{200}$ =1223

and so on

$p_{300}$ =1987

and so on

$p_{400}$ =2741

and so on

$p_{500}$ =3571

and so on

$p_{600}$ =4409

and so on

$p_{700}$ =5279

and so on

$p_{800}$ =6133

and so on

$p_{900}$ =6997

and so on

$p_{1000}$ =7919

and so on

$p_{5000}$ =48611

and so on

$p_{10000}$ =104729

to infinity

Note: As atomic number i increases, the computing time increases, so that every computer and even every high-performance computer or supercomputer in the universe sooner or later reaches its limits.

Munich, 5 October, 2024, 20 December 2024

Gottfried Färberböck