The dual prime function

PRIME NUMBER SERIES 9

Prime function p(n) provides for n ∈ ℕ greater than 0 always a prime greater than 2.

Prime function p(n) is designated dual because

the result is always prime 3 for predictable n ∈ ℕ greater than 0

and

p(n) provides all prime numbers greater than 3 for the residual n ∈ ℕ greater than 0.

The dual prime function reads:

p(n)=2n*t(n)+3

This means

$p(n)=2n\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil+3$

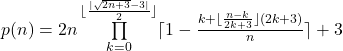
whereby n,k ∈ ℕ with n ≥ 1 and k ≥ 0.

Proof:

With the aid of the deterministic test function t(n) the t(n) is determined for a choosed n. Because t(n) can only have the values 0 for not prime and 1 for prime the results for p(n) are:

t(n)=0 → p(n)=3 → The choosed n gives in 2n+3 a composite uneven number

t(n)=1 → p(n) gives a prime > 3.

Because

2n+3 for n ∈ ℕ

provides all uneven numbers > 1 which are comprised only of all composite uneven numbers and all not composite uneven numbers (= all prime numbers > 2), all n which are in t(n)=1 must be in p(n) all prime numbers > 2.

The predictable n ∈ ℕ greater than 0 which have always in function p(n) prime 3 as result, of course must satify formula

n=n_km= 2k²+6k+3+m(2k+3) ʌ k, m ∈ ℕ

What had to be proved.

Munich, 24 October 2022

Gottfried Färberböck

THE n-PRIMALITY TEST” href=”https://dieprimzahlenserie.com/primzahltestfunktion/”>Testfunktion t(n)

wird für ein gewähltes n das t(n) ermittelt. Da t(n) nur die Werte 0 für nicht prim und 1 für prim haben kann, gibt es für p(n) folgende Ergebnismöglichkeiten:

t(n)=0 → p(n)=3 → Das gewählte n ergibt in 2n+3 eine zusammengesetzte, ungerade Zahl

t(n)=1 → p(n) ergibt eine Primzahl > 3.

2n+3 für n ∈ ℕ

alle ungeraden Zahlen > 1 liefert und diese nur aus allen zusammengesetzten, ungeraden Zahlen und allen nicht zusammengesetzten, ungeraden Zahlen (= alle Primzahlen > 2) bestehen, müssen alle n, die in t(n)=1 sind, in p(n) alle Primzahlen > 2 sein.

Die vorhersagbaren n ∈ ℕ größer 0, die immer in der Funktion p(n) die Primzahl 3 als Ergebnis haben, müssen natürlich der Formel

n=n_km= 2k²+6k+3+m(2k+3) ʌ k, m ∈ ℕ

entsprechen.

Was zu beweisen war.

München, 24. Oktober 2022

Gottfried Färberböck

Language:

Language:

THE PRIME NUMBER SERIES

The dual prime function