Language:

Language:

THE PRIME NUMBER SERIES

The next prime number

THE PRIME NUMBER SERIES 23

The next prime number

 

Let U be an odd number. The next prime number is sought.

This can be done by first determining the number of prime numbers up to U and then the first prime number following U. I split the procedure into two steps because one step would put too much strain on computers.

i=pi(U) is the number of prime numbers up to and including the odd number U. Then the following applies:

i=\pi(U)=2+\sum\limits_{n=1}^{\frac{U-3}{2}}(\prod\limits_{k=0} ^{\frac{\sqrt{2n+3}-3} {2}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)

and

p=p(U,i)=U+2*\sum\limits_{n_{max}=\frac{U-3}{2}}^{\frac{U-3}{2}+1.218\sqrt{\frac{U-3}{2}}}\lfloor(\frac{i+1}{\sum\limits_{n=1}^{n_{max}}(\prod\limits_{k=0} ^{\frac{\sqrt{2n+3}-3} {2}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)+3})^\frac{1}{i+1})\rfloor

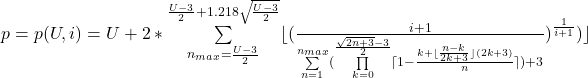
valid for U ≥ 5 ∧ U \in \mathbb{N}

Examples:

Let U=5. Subinserted into the formula for pi(U) results in i=3. I.e. up to and including the number 5 there are three prime numbers. And indeed: they are the prime numbers 2, 3 and 5. Thus, the next following prime number p can be calculated with p(5,3)=7. And 7 is actually the first larger prime number after 5.

Let U=713. Inserted into the formula for pi(U), i=127. I.e. up to and including the number 713 there are 127 prime numbers. Thus, p can be calculated as p(713,127)=719.

Tested with my prime number test

t(x)=\sum\limits_{\lceil\frac{x-3}{2}\rceil}^{\lfloor\frac{x-3}{2}\rfloor}(\prod\limits_{k=0} ^{\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)

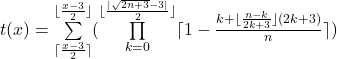
valid for x ≥ 4 ∧ x \in \mathbb{R}

results in the following values:

t(713)=0 d.h. 713 is not prime

t(715)=0 specifically 715 is not prime

t(717)=0 specifically 717 is not prime

t(719)=1 specifically 719 is prime

This proves that 719 is the first prime number that follows the odd number 713.

 

Munich, 21 April 2024

Gottfried Färberböck