The prime number function, the prime number theorem and the actual number of primes
PRIME NUMBER SERIES 15
The prime number function, the prime number theorem and the actual number of primes
The prime function ![]() is defined as the number of primes p not greater than x:
is defined as the number of primes p not greater than x:
![]() =|{
=|{![]() ∧ p ≤ x ∧
∧ p ≤ x ∧ ![]() }|
}|
Legend:
|![]() | = power of a set
| = power of a set ![]()
![]() = set of prime numbers
= set of prime numbers
![]() = set of real numbers
= set of real numbers
Gauss found a first approximation already at the age of 15:
![]() ~
~![]()
valid for x ≥ 3
This approximation was taken as the basis for the prime number theorem, which states the following:
![]()
![]() =1.
=1.
Later, even better approximations were found.
The prime function ![]() is defined as the number of primes p not greater than
is defined as the number of primes p not greater than ![]() :
:
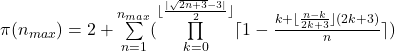
The prime function ![]() returns the exact number of all primes up to a chosen value
returns the exact number of all primes up to a chosen value ![]() for
for ![]() ∈ ℕ. Thus, it is not an approximate value, but the actual number.
∈ ℕ. Thus, it is not an approximate value, but the actual number.
Compare ![]() ~
~![]() with the actual number
with the actual number ![]() :
:
| x | Actual number | Deviation | ||
| 10 | 3 | 4 | 4 | 0 |
| 100 | 48 | 21 | 25 | 4 |
| 1000 | 498 | 144 | 168 | 24 |
| 10000 | 4998 | 1085 | 1229 | 144 |
| 100000 | 49998 | 8685 | 9592 | 907 |
| 1000000 | 499998 | 72382 | 78498 | 6116 |
Munich, March 11, 2023
Gottfried Färberböck


