An exact prime number function

THE PRIME NUMBER SERIES 19

The prime number function $\pi(x)$ is defined as the number of all prime numbers that is less than or equal to the real number x.

For at least 200 years, mathematicians have tried to find the best possible approximations of the prime number function, starting with Gauss to Legendre, Chebyshov, Sylvester, Riemann and others.

At least one exact prime number function that does not require approximations and always specifies the correct number of prime numbers for each x less than or equal to the real number x is

$\pi(x})=2+\sum\limits_{n=1}^{\frac{x-3}{2}}(\prod\limits_{k=0} ^{{\frac{\sqrt{2n+3}-3} {2}}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

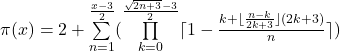
valid for x ≥ 3 ∧ x $\in \mathbb{R}$

Below is a comparison of the Riemann approximation formula R(x) with my exact formula F(x) and the actual number $\pi(x})$ :

x	$\pi(x)$	F(x)	R(x)	Riemann-deviation
100	25	25	26	1
1000	168	168	168	0
10000	1229	1229	1227	-2
100000	9592	9592	9587	-5
1000000	78498	78498	78527	29

Since the calculation time for increasing x is getting longer and longer, or it can be interesting how many prime numbers are in an arbitrary number range, the following function can be used:

$\pi(x_{min},x_{max}})=\sum\limits_{\lceil\frac{x_{min}-3}{2}\rceil}^{\frac{x_{max}-3}{2}}(\prod\limits_{k=0} ^{{\frac{\sqrt{2n+3}-3} {2}}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil)$

valid for $x_{min},x_{max}$ ≥ 4 ∧ $x_{min},x_{max}$ $\in \mathbb{R}$

Munich, 5.April 2024

Gottfried Färberböck

Language:

Language:

THE PRIME NUMBER SERIES

An exact prime number function