Infinite prime number formulas thanks to Eratosthenes

PRIME NUMBER SERIES 13

There are infinitely many prime number formulas. Every single one of these formulas returns exclusively prime numbers in predetermined ranges and, moreover, all prime numbers besides 3 which exist at all in the respective range.

These are bold assertions.

In PRIME NUMBER SERIES 9, THE DUAL PRIME FUNCTION was proven:

Prime function p(n) provides for n ∈ ℕ greater than 0 always a prime greater than 2.

The result of prime function p(n) is always prime 3 for predictable n ∈ ℕ greater than 0 and for the residual n ∈ ℕ greater than 0 ALL PRIME NUMBERS GREATER THAN 3.

The dual prime function is:

p(n)=2n*t(n)+3

In PRIME NUMBER SERIES 7, THE n-PRIMALITY TEST was proven:

t(n) is either 0 or 1 for a choosed n>0 from the set of the natural numbers.

If t(n)=0, then 2n+3 is not prime for the choosed n.

If t(n)=1, then 2n+3 is prime for the choosed n.

$t(n)=\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

with

$k_{max}=\lfloor{\frac{|\sqrt{2n+3}-3|} {2}\rfloor}$

where n ∈ ℕ and n ≥ 1 and k ∈ ℕ and k ≥ 0.

In p(n) and in t(n), n is the variable and $k_{max}$ is the dependent variable.

What happens if $k_{max}$ ∈ ℕ is a free-choice variable and n ∈ ℕ ≥ 1 is an upper bounded variable?

If we set $k_{max}$ as a variable in p(n), this results in

p( $k_{max},n$ )=2n*t( $k_{max}$ )+3

This can also be written as:

p( $k_{max},n$ )=3+2n*t( $k_{max}$ )

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

The basis for all prime numbers greater than 2 is the potential prime function

p_pot (n)=2n+3 ∧ n ∈ ℕ

This function returns all odd numbers greater than 1 consisting of all prime numbers greater than 2 and all composite odd numbers.

The infinite sequence of numbers for p_pot(n) is:

3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,
39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,
71,73,75,77,79,81,83….

Now we sieve by means of the function p( $k_{max},n$ ) similar to the sieve of Eratosthenes or even more similar to THE ODD SIEVE. However, a 3 takes the place of the deleted number in each case.

If $k_{max}$ =0, for n ∈ ℕ and $n_{min}$ =1 this results in the infinite sequence of numbers

5,7,3,11,13,3,17,19,3,23,25,3,29,31,3,35,37,3,41,
43,3,47,49,3,53,55,3,59,61,3,65,67,3,71,73,3,77,79,
3,83….

In this sequence of numbers, all numbers divisible by 3 are screened out by converting each to the number 3 from 2n*0+3.

Further we can see that all numbers smaller than 25=5² are prime.

This gives the 1st prime formula

$p_{1}=3+2n\lceil1-3\frac{\lfloor\frac{n}{3}\rfloor)}{n}\rceil$

valid for $1 \le n \le 10$

And then there is one more thing: The smallest prime number except 3 is 5.

The next sieving with $k_{max}$ =1 and $n_{min}$ =2 gives the infinite sequence of numbers

7,3,11,13,3,17,19,3,23,3,3,29,31,3,3,37,3,41,43,3,
47,49,3,53,3,3,59,61,3,3,67,3,71,73,3,77,79,3,83,….

In this infinite number sequence, all numbers divisible by 3 and 5 are screened out.

Further we can see that all numbers smaller than 49=7² are prime.

This gives the 2nd prime formula

$p_{2}=3+2n\lceil1-3\frac{\lfloor\frac{n}{3}\rfloor}{n}\rceil\lceil1-\frac{1+5\lfloor\frac{n-1}{5}\rfloor}{n}\rceil$

valid for $2 \le n \le 22$

And the smallest prime number except 3 is 7.

Oops! Are there any regularities in this?

Let’s check further by arbitrarily setting $k{max}$ =5.

The resulting infinite sequence of numbers should therefore not contain any composite number divisible by 3 and no numbers divisible by 5,7,9,11 and 13. Furthermore, all numbers smaller than 15²=225 would have to be prime. And furthermore the smallest prime number except 3 would have to be 17, because

$n_{min}=k_{max}+1$

$n_{min}$ =5+1=6

Is that really the case?

We put $k_{max}$ =5 in p( $k_{max},n$ ) and obtain the 6th formula

$p_{6}=3+2n \lceil1-3\frac{\lfloor\frac{n}{3}\rfloor}n}\rceil \lceil1-\frac{1+5\lfloor\frac{n-1}{5}\rfloor}{n}\rceil \lceil1-\frac{2+7\lfloor\frac{n-2}{7}\rfloor}{n}\rceil$ $\lceil1-\frac{3+9\lfloor\frac{n-3}{9}\rfloor}{n}\rceil \lceil1-\frac{4+11\lfloor\frac{n-4}{11}\rfloor}{n}\rceil \lceil1-\frac{5+13\lfloor\frac{n-5}{13}\rfloor}{n}\rceil$

and obtain for n from

$n_{min}=6$

the infinite sequence of numbers

3,17,19,3,23,3,3,29,31,3,3,37,3,41,43,3,47,
3,3,53,3,3,59,61,3,3,67,3,71,73,3,3,79,3,83,3,3,89,3,
3,3,97,3,101,103,3,107,109,3,113,3,3,3,3,3,3,127,3,
131,3,3,137,139,3,3,3,3,149,151,3,3,157,3,3,163,3,
167,3,3,173,3,3,179,181,3,3,3,3,191,193,3,197,199,
3,3,3,3,3,211,3,3,3,3,3,223,3,227,229,3,233,3,3,239,
241,3,3,3,3,251,3,3,257,3,3,263,3,3,269,271,3,3,277,
3,281,283,3,3,289,3,293,3,3,3,3,3,3,307,3,311,313,3,
317,3,3,323,3,3,3,331,3,3,337,3,3,3,3,347,349,3,353,
3,3,359,361,3,3,367,3,3,373,3,3,379,3,383,3,3,389,
391,3,3,397,3,401,3,….

And indeed:

The smallest prime number except 3 is 17.

All numbers smaller than 15²=225 are prime.

Thus the 6th formula is the 6th prime number formula.

In fact, all numbers smaller than 17²=289 are prime. The reason for this is that 15 is divisible and 17 is the next prime number after 13.

With regard to the resulting infinite sequence of numbers, there should be no more numbers divisible by 3,5,7,9,11 and 13 except for the 3-digits which replace composite numbers. And indeed: All composite numbers divisible by 3 and all numbers divisible by 5,7,9,11 and 13 are screened out, i.e. replaced by 3.

For the further proof we put

$s(k,n)=\lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

and denote s(k,n) as a sieve factor function.

Assertion : The sieve factor function s(k,n) can only take the values 0 or 1.

If the sieve factor function s(k,n) has the value 0, then both 2n+3 and n-k are divisible by 2k+3.

If the sieve factor function s(k,n) has the value 1, then neither 2n+3 nor n-k are divisible by 2k+3.

Proof:

In PRIME NUMBER SERIES 6 THE DETERMINATION OF ALL PRIMIAL NUMBERS IN A CHOSEN AREA WITH THE n-METHOD it was proved that in the case of

n=n_km= 2k²+6k+3+m(2k+3) ʌ k, m ∈ ℕ

n in

2n+3 ʌ n ∈ ℕ

returns all odd composite numbers and in the case of

n≠n_km

n in 2n+3 returns all primes greater than 2.

Case 1: s(k,n)=0

Proof 1: In this case must be n=n_km.

n=n_km=2k²+6k+3+m(2k+3) used in

$s(k,n)=\lceil1-\frac{k+\lfloor\frac{2k^2+6k+3+m(2k+3)-k}{2k+3}\rfloor(2k+3)}{2k^2+6k+3+m(2k+3)}\rceil$

$s(k,n)=\lceil1-\frac{k+(k+1+m)(2k+3)}{2k^2+6k+3+m(2k+3)}\rceil$

$s(k,n)=\lceil1-\frac{2k^2+6k+3+m(2k+3)}{2k^2+6k+3+m(2k+3)}\rceil$

$s(k,n)=\lceil1-1\rceil$

$s(k,n)=0$

What had to be proven.

Proof 2: If n-k is divisible by 2k+3, then the product is

$\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}=n-k$

This gives in s(k,n)

$s(k,n)=\lceil1-\frac{k+n-k}{n}\rceil$

$s(k,n)=\lceil1-\frac{n}{n}\rceil$

$s(k,n)=\lceil1-1\rceil$

$s(k,n)=0$

What had to be proven.

Case 2: s(k,n)=1

This means n-k is not divisible by 2k+3.

Proof:

If n-k is not divisible by 2k+3, the product with n>k is

$0\le\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}<n-k$

Is n really always greater than k?

Since

$n_{min}=k_{max}+1$

$n_{min}>k_{max}\ge k$

And that means further:

Any

$n>n_{min}>k_{max}>k$

So it is true that n is always greater than k. Thus applies

$0\le\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}<n-k$

If we add k to each term, this gives:

$k\le k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}<n$

If we divide each term by n≥1, this gives:

$\frac{k}{n}\le\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}<1$

Since k<n holds

$0\le\frac{k}{n}<1$

and

$0\le\frac{k}{n}<\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}<1$

$s(k,n)=\lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil=1$

What had to be proven.

Thus, this term is able to sieve out any odd composite number depending on k.

This proves that any infinite sequence of numbers for all n≥1 in

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

cannot contain a composite odd number divisible by 2k+3 from k=0 to $k=k_{max}$ .

Now we have to investigate whether in every sequence of numbers $p(k_{max},n)$ with $n_{min}$ ≤ n ≤ $n_{max}$

where

$n_{min}=k_{max}+1$

and

$n_{max}=2k_{max}^2+10k_{max}+10$

besides the 3 exclusively and all prime numbers are contained, which exist in this range. For the 1st, 2nd and 6th prime number formula this is true in all cases. But there are infinitely many other cases.

First to $k_{max}=0$ . From this follows the 1st prime number formula, for which the proof was already given.

Let us assume that the assertions are true that

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil$

in the range

$n_{min}=k_{max}+1$

and

$n_{max}=2k_{max}^2+10k_{max}+10$

for $k_{max}$ exclusively returns prime numbers and besides 3 all prime numbers which exist in this range at all.

If this is also true for $k_{max}+1$ , the proof would be complete.

For this we set

$k_{max}+1$

$p(k_{max}+1,n)=3+2n\prod\limits_{k=0} ^{k_{max}+1} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil=\lceil1-\frac{0+\lfloor\frac{n-0}{2*0+3}\rfloor(2*0+3)}{n}\rceil\lceil1-\frac{1+\lfloor\frac{n-1}{2*1+3}\rfloor(2*1+3)}{n}\rceil\lceil1-\frac{2+\lfloor\frac{n-2}{2*2+3}\rfloor(2*2+3)}{n}\rceil\lceil1-\frac{3+\lfloor\frac{n-3}{2*3+3}\rfloor(2*3+3)}{n}\rceil.........\lceil1-\frac{k_{max}+\lfloor\frac{n-k_{max}}{2*k_{max}+3}\rfloor(2*k_{max}+3)}{n}\rceil\lceil1-\frac{(k_{max}+1)+\lfloor\frac{n-(k_{max}+1)}{2*(k_{max}+1)+3}\rfloor(2*(k_{max}+1)+3)}{n}\rceil$

$p(k_{max}+1,n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3)}{n}\rceil\lceil1-\frac{(k_{max}+1)+\lfloor\frac{n-(k_{max}+1)}{2*(k_{max}+1)+3}\rfloor(2*(k_{max}+1)+3)}{n}\rceil$

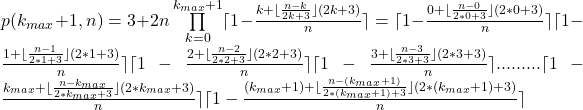
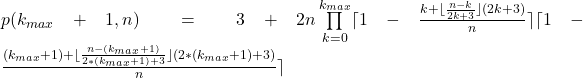
Now it is checked if there is an odd number up to

$u_{max}=(2k_{max} +5)^2-2=4k_{max}^2+20k_{max}+23=(2n_{max}+3)-2=2(2k_{max}^2+10k_{max}+10)+3=4k_{max}^2+20k_{max}+23$

which is divisible by $2k_{max}+3$ .

For this we transform

$4k_{max}^2+20k_{max}+23=4k_{max}^2+20k_{max}+21+2$

Since

$(4k_{max}^2+20k_{max}+21)/(2k_{max}+3)=2k_{max}+7$

and

$2/(2k_{max}+3)$ für $k_{max}$ ∈ ℕ

is never divisible, also

$4k_{max}^2+20k_{max}+23$

is never divisible by

$2k_{max}+3$

What had to be proven.

Thus:

The function

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

yields infinitely many formulas depending on k_{max} ∈ ℕ and k ≥ 0. Each individual formula yields, besides the prime 3, all primes in the range of n ∈ ℕ and n ≥ 1 with

$k_{max}+1 \le n \le ((2k_{max} +5)²-2-3)/2$

$k_{max}+1 \le n \le 2k_{max}^2+10k_{max}+10$

NOTES: The function $p(k_{max},n)$ can be optimized by simply omitting the composite sieve factors so that only the prime sieve factors remain. However, it must be ensured that no prime sieve factor is deleted, otherwise the results are not one hundred percent. If the prime numbers in the required range are not known, the deletion of the unnecessary sieve factors can be done, for example, with the help of the odd sieve, by deleting all p² (starting at 3²=9) and all p.th sieve factors following p² or simply omitting them. The respective p.th value is also obtained by adding 2p from p².

The larger $k_{max}$ is chosen, the more and larger prime numbers are supplied. This goes so far that even the strongest computer that will ever exist will not be able to calculate them.

TASKS

Task 1: What is the upper bound for all prime formulas that can be derived from the function $p(k_{max},n)$ ? What is this for the tenth prime formula?

$n_{max}=2k_{max}^2+10k_{max}+10$

$k_{max}=10-1=9$

$n_{max}=2*9^2+10*9+10=262$

Task 2: What is the lower bound for all prime formulas that can be derived from the function $p(k_{max},n)$ ? What is it for the tenth prime formula?

$n_{min}=k_{max}+1$

For the tenth prime formula, this is:

$n_{min}=k_{max}+1=9+1=10$

Task 3: What is the smallest potential prime number greater than 3 of a prime number formula that yields all primes in this range? Specifically, what are these for the tenth prime formula?

The lower bound for the smallest prime number greater than 3 can be derived from

$n_{min}=k_{max}+1$

$p_{min}>2n_{min}+1$

$p_{min}>2(k_{max}+1)+1$

$p_{min}>2k_{max}+3$

In the case of the tenth prime formula $k_{max}=9$ . This results in

$p_{min}>2*9+3$

$p_{min}>21$

Task 4: What is the largest potential prime of a prime formula that yields all primes in this range? Specifically, what is this for the tenth prime formula?

The upper bound for the largest potential prime can be derived from

$n_{max}=2k_{max}^2+10k_{max}+10$

$p_{pot}{_{max}}=2(2k_{max}^2+10k_{max}+10)+3$

$p_{pot}{_{max}}=4k_{max}^2+20k_{max}+23$

In the case of the tenth prime formula $k_{max}=9$ . This results in

$p_{pot}{_{max}}=4*(9)^2+20*9+23=324+180+23=527$

Task 5: In what range does any prime formula derived from the function $p(k_{max},n)$ return all numbers that are prime? Specifically, what is this range for the tenth prime formula?

Answer:

2 $k_{max}$ +4 < p < 4 $k_{max}$ ² +20 $k_{max}$ +24

The tenth prime formula yields in the range

22<p<528

exclusively prime numbers and moreover these are all prime numbers which exist in this range.

Task 6: What is the function from which infinitely many prime number formulas can be derived? In which range do the derived prime number formulas apply?

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

$n_{min} \le n \le n_{max}$

$n_{min}=k_{max}+1$

$n_{max}=2k_{max}^2+10k_{max}+10$

Task 7: Determine the tenth prime formula.

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

$k_{max}=10-1=9$

$p(9,n)=3+2n\prod\limits_{k=0}^{9} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

$p_{10}=3+2n$ $\lceil1-3\frac{\lfloor\frac{n}{3}\rfloor}{n}\rceil\lceil1-\frac{1+5\lfloor\frac{n-1}{5}\rfloor}{n}\rceil\lceil1-\frac{2+7\lfloor\frac{n-2}{7}\rfloor}{n}\rceil\lceil1-\frac{3+9\lfloor\frac{n-3}{9}\rfloor}{n}\rceil$

$\lceil1-\frac{4+11\lfloor\frac{n-4}{11}\rfloor}{n}\rceil\lceil1-\frac{5+13\lfloor\frac{n-5}{13}\rfloor}{n}\rceil\lceil1-\frac{6+15\lfloor\frac{n-6}{15}\rfloor}{n}\rceil\lceil1-\frac{7+17\lfloor\frac{n-7}{17}\rfloor}{n}\rceil\lceil1-\frac{8+19\lfloor\frac{n-8}{19}\rfloor}{n}\rceil$

$\lceil1-\frac{9+21\lfloor\frac{n-9}{21}\rfloor}{n}\rceil$

Task 8: Determine the prime sequence of the tenth prime formula.

23,3,3,29,31,3,3,37,3,41,43,3,47,3,3,53,3,3,59,61,3,3,
67,3,71,73,3,3,79,3,83,3,3,89,3,3,3,97,3,101,103,3,107,
109,3,113,3,3,3,3,3,3,127,3,131,3,3,137,139,3,3,3,3,
149,151,3,3,157,3,3,163,3,167,3,3,173,3,3,179,181,3,
3,3,3,191,193,3,197,199,3,3,3,3,3,211,3,3,3,3,3,223,3,
227,229,3,233,3,3,239,241,3,3,3,3,251,3,3,257,3,3,
263,3,3,269,271,3,3,277,3,281,283,3,3,3,3,293,3,3,3,3,
3,3,307,3,311,313,3,317,3,3,3,3,3,3,331,3,3,337,3,3,3,
3,347,349,3,353,3,3,359,3,3,3,367,3,3,373,3,3,379,3,
383,3,3,389,3,3,3,397,3,401,3,3,3,409,3,3,3,3,419,421,
3,3,3,3,431,433,3,3,439,3,443,3,3,449,3,3,3,457,3,461,
463,3,467,3,3,3,3,3,479,3,3,3,487,3,491,3,3,3,499,3,
503,3,3,509,3,3,3,3,3,521,523,3,3

Task 9: Determine the optimized tenth prime formula. With optimized prime number formula is meant that from the prime number formula those sieve factors were removed, with which 2k+3 is a compound number. I.e. actually only those sieve factors are needed for which 2k+3 is prime.

$p_{10}=3+2n$ $\lceil1-3\frac{\lfloor\frac{n}{3}\rfloor}{n}\rceil\lceil1-\frac{1+5\lfloor\frac{n-1}{5}\rfloor}{n}\rceil\lceil1-\frac{2+7\lfloor\frac{n-2}{7}\rfloor}{n}\rceil$

$\lceil1-\frac{4+11\lfloor\frac{n-4}{11}\rfloor}{n}\rceil\lceil1-\frac{5+13\lfloor\frac{n-5}{13}\rfloor}{n}\rceil\lceil1-\frac{7+17\lfloor\frac{n-7}{17}\rfloor}{n}\rceil\lceil1-\frac{8+19\lfloor\frac{n-8}{19}\rfloor}{n}\rceil$

Task 10: Determine the prime sequence of the tenth prime formula without the prime 3.

23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,
101,103,107,109,113,127,131,137,139,149,151,157,
163,167,173,179,181,191,193,197,199,211,223,227,
229,233,239,241,251,257,263,269,271,277,281,283,
293,307,311,313,317,331,337,347,349,353,359,367,
373,379,383,389,397,401,409,419,421,431,433,439,
443,449,457,461,463,467,479,487,491,499,503,509,
521,523

Task 11: Determine the hundredth prime formula and the corresponding prime sequence.

$p(k_{max},n)=3+2n\prod\limits_{k=0} ^{k_{max}} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

$k_{max}=99$

$p(99,n)=3+2n\prod\limits_{k=0}^{99} \lceil1-\frac{(k+\lfloor\frac{n-k}{2k+3}\rfloor(2k+3))}{n}\rceil$

$p_{100}=3+2n$ $\lceil1-3\frac{\lfloor\frac{n}{3}\rfloor}{n}\rceil\lceil1-\frac{1+5\lfloor\frac{n-1}{5}\rfloor}{n}\rceil\lceil1-\frac{2+7\lfloor\frac{n-2}{7}\rfloor}{n}\rceil$ …….

$\lceil1-\frac{98+199\lfloor\frac{n-98}{199}\rfloor}{n}\rceil \lceil1-\frac{99+201\lfloor\frac{n-99}{201}\rfloor}{n}\rceil$

100 ≤ n ≤ 20602

The prime sequence for the hundredth prime formula is

3,3,3,3,211,3,3,3,3,3,223,3,227,229,3,233,3,3,239,
241,3,3,3,3,251,3,3,257,3,3,263,3,3,269,271,3,3,277,
3,281,283,3,3,3,3,293,3,3,3,3,3,3,307,3,311,313,3,
317,3,3,3,3,3,3,331,3,3,337,3,3,3,3,347,349,3,353,3,
3,359,3,3,3,367,3,3,373,3,3,379,3,383,3,3,389,3,3,3,
397,3,401,3,3,3,409,3,3,3,3,419,421,3,3,3,3,431,433,
3,3,439,3,443,3,3,449,3,3,3,457,3,461,463,3,467,3,3,
3,3,3,479,3,3,3,487,3,491,3,3,3,499,3,503,3,3,509,3,
3,3,3,3,521,523,3,3,3,3,3,3,3,3,541,3,3,547,3,3,3,3,
557,3,3,563,3,3,569,571,3,3,577,3,3,3,3,587,3,3,593,
3,3,599,601,3,3,607,3,3,613,3,617,619,3,3,3,3,3,631,
3,3,3,3,641,643,3,647,3,3,653,3,3,659,661,3,3,3,3,3,
673,3,677,3,3,683,3,3,3,691,3,3,3,3,701,3,3,3,709,3,
3,3,3,719,3,3,3,727,3,3,733,3,3,739,3,743,3,3,3,751,
3,3,757,3,761,3,3,3,769,3,773,3,3,3,3,3,3,787,3,3,3,3,
797,3,3,3,3,3,809,811,3,3,3,3,821,823,3,827,829,3,3,
3,3,839,3,3,3,3,3,3,853,3,857,859,3,863,3,3,3,3,3,3,
877,3,881,883,3,887,3,3,3,3,3,3,3,3,3,907,3,911,3,3,3,
919,3,3,3,3,929,3,3,3,937,3,941,3,3,947,3,3,953,3,3,
3,3,3,3,967,3,971,3,3,977,3,3,983,3,3,3,991,3,3,997,
3,3,3,3,3,1009,3,1013,3,3,1019,1021,3,3,3,3,1031,
1033,3,3,1039,3,3,3,3,1049,1051,3,3,3,3,1061,1063,3,
3,1069,3,3,3,3,3,3,3,3,1087,3,1091,1093,3,1097,3,3,
1103,3,3,1109,3,3,3,1117,3,3,1123,3,3,1129,3,3,3,3,3,
3,3,3,3,3,1151,1153,3,3,3,3,1163,3,3,3,1171,3,3,3,3,
1181,3,3,1187,3,3,1193,3,3,3,1201,3,3,3,3,3,1213,3,
1217,3,3,1223,3,3,1229,1231,3,3,1237,3,3,3,3,3,1249,
3,3,3,3,1259,3,3,3,3,3,3,3,3,1277,1279,3,1283,3,3,
1289,1291,3,3,1297,3,1301,1303,3,1307,3,3,3,3,3,
1319,1321,3,3,1327,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
1361,3,3,1367,3,3,1373,3,3,3,1381,3,3,3,3,3,3,3,3,
1399,3,3,3,3,1409,3,3,3,3,3,3,1423,3,1427,1429,3,
1433,3,3,1439,3,3,3,1447,3,1451,1453,3,3,1459,3,3,3,
3,3,1471,3,3,3,3,1481,1483,3,1487,1489,3,1493,3,3,
1499,3,3,3,3,3,1511,3,3,3,3,3,1523,3,3,3,1531,3,3,3,3,
3,1543,3,3,1549,3,1553,3,3,1559,3,3,3,1567,3,1571,3,
3,3,1579,3,1583,3,3,3,3,3,3,1597,3,1601,3,3,1607,
1609,3,1613,3,3,1619,1621,3,3,1627,3,3,3,3,1637,3,3,
3,3,3,3,3,3,3,1657,3,3,1663,3,1667,1669,3,3,3,3,3,3,
3,3,3,3,3,1693,3,1697,1699,3,3,3,3,1709,3,3,3,3,3,
1721,1723,3,3,3,3,1733,3,3,3,1741,3,3,1747,3,3,1753,
3,3,1759,3,3,3,3,3,3,3,3,1777,3,3,1783,3,1787,1789,
3,3,3,3,3,1801,3,3,3,3,1811,3,3,3,3,3,1823,3,3,3,1831,
3,3,3,3,3,3,3,1847,3,3,3,3,3,3,1861,3,3,1867,3,1871,
1873,3,1877,1879,3,3,3,3,1889,3,3,3,3,3,1901,3,3,
1907,3,3,1913,3,3,3,3,3,3,3,3,1931,1933,3,3,3,3,3,3,
3,1949,1951,3,3,3,3,3,3,3,3,3,3,1973,3,3,1979,3,3,3,
1987,3,3,1993,3,1997,1999,3,2003,3,3,3,2011,3,3,
2017,3,3,3,3,2027,2029,3,3,3,3,2039,3,3,3,3,3,3,
2053,3,3,3,3,2063,3,3,2069,3,3,3,3,3,2081,2083,3,
2087,2089,3,3,3,3,2099,3,3,3,3,3,2111,2113,3,3,3,3,3,
3,3,2129,2131,3,3,2137,3,2141,2143,3,3,3,3,2153,3,3,
3,2161,3,3,3,3,3,3,3,3,2179,3,3,3,3,3,3,3,3,3,3,3,
2203,3,2207,3,3,2213,3,3,3,2221,3,3,3,3,3,3,3,2237,
2239,3,2243,3,3,3,2251,3,3,3,3,3,3,3,2267,2269,3,
2273,3,3,3,2281,3,3,2287,3,3,2293,3,2297,3,3,3,3,3,
2309,2311,3,3,3,3,3,3,3,3,3,3,2333,3,3,2339,2341,3,3,
2347,3,2351,3,3,2357,3,3,3,3,3,3,2371,3,3,2377,3,
2381,2383,3,3,2389,3,2393,3,3,2399,3,3,3,3,3,2411,3,
3,2417,3,3,2423,3,3,3,3,3,3,2437,3,2441,3,3,2447,3,
3,3,3,3,2459,3,3,3,2467,3,3,2473,3,2477,3,3,3,3,3,3,
3,3,3,3,3,3,2503,3,3,3,3,3,3,3,3,2521,3,3,3,3,2531,3,
3,3,2539,3,2543,3,3,2549,2551,3,3,2557,3,3,3,3,3,3,
3,3,3,3,2579,3,3,3,3,3,2591,2593,3,3,3,3,3,3,3,2609,
3,3,3,2617,3,2621,3,3,3,3,3,2633,3,3,3,3,3,3,2647,3,
3,3,3,2657,2659,3,2663,3,3,3,2671,3,3,2677,3,3,
2683,3,2687,2689,3,2693,3,3,2699,3,3,3,2707,3,2711,
2713,3,3,2719,3,3,3,3,2729,2731,3,3,3,3,2741,3,3,3,
2749,3,2753,3,3,3,3,3,3,2767,3,3,3,3,2777,3,3,3,3,3,
2789,2791,3,3,2797,3,2801,2803,3,3,3,3,3,3,3,2819,3,
3,3,3,3,3,2833,3,2837,3,3,2843,3,3,3,2851,3,3,2857,
3,2861,3,3,3,3,3,3,3,3,2879,3,3,3,2887,3,3,3,3,2897,
3,3,2903,3,3,2909,3,3,3,2917,3,3,3,3,2927,3,3,3,3,3,
2939,3,3,3,3,3,3,2953,3,2957,3,3,2963,3,3,2969,2971,
3,3,3,3,3,3,3,3,3,3,3,3,3,2999,3001,3,3,3,3,3011,3,3,3,
3019,3,3023,3,3,3,3,3,3,3037,3,3041,3,3,3,3049,3,3,
3,3,3,3061,3,3,3067,3,3,3,3,3,3079,3,3083,3,3,3089,
3,3,3,3,3,3,3,3,3,3109,3,3,3,3,3119,3121,3,3,3,3,3,3,3,
3137,3,3,3,3,3,3,3,3,3,3,3,3,3163,3,3167,3169,3,3,3,
3,3,3181,3,3,3187,3,3191,3,3,3,3,3,3203,3,3,3209,3,
3,3,3217,3,3221,3,3,3,3229,3,3,3,3,3,3,3,3,3,3,3251,
3253,3,3257,3259,3,3,3,3,3,3271,3,3,3,3,3,3,3,3,3,3,
3,3,3,3299,3301,3,3,3307,3,3,3313,3,3,3319,3,3323,3,
3,3329,3331,3,3,3,3,3,3343,3,3347,3,3,3,3,3,3359,
3361,3,3,3,3,3371,3373,3,3,3,3,3,3,3,3389,3391,3,3,
3,3,3,3,3,3407,3,3,3413,3,3,3,3,3,3,3,3,3,3433,3,3,3,
3,3,3,3,3449,3,3,3,3457,3,3461,3463,3,3467,3469,3,3,
3,3,3,3,3,3,3,3,3491,3,3,3,3499,3,3,3,3,3,3511,3,3,
3517,3,3,3,3,3527,3529,3,3533,3,3,3539,3541,3,3,
3547,3,3,3,3,3557,3559,3,3,3,3,3,3571,3,3,3,3,3581,
3583,3,3,3,3,3593,3,3,3,3,3,3,3607,3,3,3613,3,3617,
3,3,3623,3,3,3,3631,3,3,3637,3,3,3643,3,3,3,3,3,3,3,
3659,3,3,3,3,3,3671,3673,3,3677,3,3,3,3,3,3,3691,3,
3,3697,3,3701,3,3,3,3709,3,3,3,3,3719,3,3,3,3727,3,
3,3733,3,3,3739,3,3,3,3,3,3,3,3,3,3,3761,3,3,3767,
3769,3,3,3,3,3779,3,3,3,3,3,3,3793,3,3797,3,3,3803,
3,3,3,3,3,3,3,3,3821,3823,3,3,3,3,3833,3,3,3,3,3,3,
3847,3,3851,3853,3,3,3,3,3863,3,3,3,3,3,3,3877,3,
3881,3,3,3,3889,3,3,3,3,3,3,3,3,3907,3,3911,3,3,3917,
3919,3,3923,3,3,3929,3931,3,3,3,3,3,3943,3,3947,3,3,
3,3,3,3,3,3,3,3967,3,3,3,3,3,3,3,3,3,3,3989,3,3,3,3,3,
4001,4003,3,4007,3,3,4013,3,3,4019,4021,3,3,4027,3,
3,3,3,3,3,3,3,3,3,4049,4051,3,3,4057,3,3,3,3,3,3,3,
4073,3,3,4079,3,3,3,3,3,4091,4093,3,3,4099,3,3,3,3,
3,4111,3,3,3,3,3,3,3,4127,4129,3,4133,3,3,4139,3,3,3,
3,3,3,4153,3,4157,4159,3,3,3,3,3,3,3,3,4177,3,3,3,3,
3,3,3,3,3,3,3,4201,3,3,3,3,4211,3,3,4217,4219,3,3,3,3,
4229,4231,3,3,3,3,4241,4243,3,3,3,3,4253,3,3,4259,
4261,3,3,3,3,4271,4273,3,3,3,3,4283,3,3,4289,3,3,3,
4297,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4327,3,3,3,3,4337,
4339,3,3,3,3,4349,3,3,3,4357,3,3,4363,3,3,3,3,4373,
3,3,3,3,3,3,3,3,4391,3,3,4397,3,3,3,3,3,4409,3,3,3,3,
3,4421,4423,3,3,3,3,3,3,3,3,4441,3,3,4447,3,4451,3,
3,4457,3,3,4463,3,3,3,3,3,3,3,3,4481,4483,3,3,3,3,
4493,3,3,3,3,3,3,4507,3,3,4513,3,4517,4519,3,4523,3,
3,3,3,3,3,3,3,3,3,3,4547,4549,3,3,3,3,3,4561,3,3,
4567,3,3,3,3,3,3,3,4583,3,3,3,4591,3,3,4597,3,3,
4603,3,3,3,3,3,3,3,3,4621,3,3,3,3,3,3,3,4637,4639,3,
4643,3,3,4649,4651,3,3,4657,3,3,4663,3,3,3,3,4673,3,
3,4679,3,3,3,3,3,4691,3,3,3,3,3,4703,3,3,3,3,3,3,3,3,
4721,4723,3,3,4729,3,4733,3,3,3,3,3,3,3,3,4751,3,3,
3,4759,3,3,3,3,3,3,3,3,3,3,3,4783,3,4787,4789,3,
4793,3,3,4799,4801,3,3,3,3,3,4813,3,4817,3,3,3,3,3,
3,4831,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4861,3,3,3,3,4871,
3,3,4877,3,3,3,3,3,4889,3,3,3,3,3,3,4903,3,3,4909,3,
3,3,3,4919,3,3,3,3,3,4931,4933,3,4937,3,3,4943,3,3,
3,4951,3,3,4957,3,3,3,3,4967,4969,3,4973,3,3,3,3,3,
3,4987,3,3,4993,3,3,4999,3,5003,3,3,5009,5011,3,3,3,
3,5021,5023,3,3,3,3,3,3,3,5039,3,3,3,3,3,5051,3,3,3,
5059,3,3,3,3,3,3,3,3,5077,3,5081,3,3,5087,3,3,3,3,3,
5099,5101,3,3,5107,3,3,5113,3,3,5119,3,3,3,3,3,3,3,3,
3,3,3,3,3,5147,3,3,5153,3,3,3,3,3,3,5167,3,5171,3,3,
3,5179,3,3,3,3,5189,3,3,3,5197,3,3,3,3,3,5209,3,3,3,
3,3,3,3,3,5227,3,5231,5233,3,5237,3,3,3,3,3,3,3,3,3,
3,3,5261,3,3,3,3,3,5273,3,3,5279,5281,3,3,3,3,3,3,3,
5297,3,3,5303,3,3,5309,3,3,3,3,3,3,5323,3,3,3,3,
5333,3,3,3,3,3,3,5347,3,5351,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,5381,3,3,5387,3,3,5393,3,3,5399,3,3,3,5407,3,3,
5413,3,5417,5419,3,3,3,3,3,5431,3,3,5437,3,5441,
5443,3,3,5449,3,3,3,3,3,3,3,3,3,3,5471,3,3,5477,
5479,3,5483,3,3,3,3,3,3,3,3,5501,5503,3,5507,3,3,3,
3,3,5519,5521,3,3,5527,3,5531,3,3,3,3,3,3,3,3,3,3,3,
3,5557,3,3,5563,3,3,5569,3,5573,3,3,3,5581,3,3,3,3,
5591,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,5623,3,3,3,3,3,3,3,
5639,5641,3,3,5647,3,5651,5653,3,5657,5659,3,3,3,3,
5669,3,3,3,3,3,3,5683,3,3,5689,3,5693,3,3,3,5701,3,
3,3,3,5711,3,3,5717,3,3,3,3,3,3,3,3,3,5737,3,5741,
5743,3,3,5749,3,3,3,3,3,3,3,3,3,3,3,3,3,3,5779,3,
5783,3,3,3,5791,3,3,3,3,5801,3,3,5807,3,3,5813,3,3,
3,5821,3,3,5827,3,3,3,3,3,5839,3,5843,3,3,5849,5851,
3,3,5857,3,5861,3,3,5867,5869,3,3,3,3,5879,5881,3,3,
3,3,3,3,3,5897,3,3,5903,3,3,3,3,3,3,3,3,3,5923,3,
5927,3,3,3,3,3,5939,3,3,3,3,3,3,5953,3,3,3,3,3,3,3,3,
3,3,3,3,3,5981,3,3,5987,3,3,3,3,3,3,3,3,3,6007,3,6011,
3,3,3,3,3,3,3,3,6029,3,3,3,6037,3,3,6043,3,6047,3,3,
6053,3,3,3,3,3,3,6067,3,3,6073,3,3,6079,3,3,3,3,
6089,6091,3,3,3,3,6101,3,3,3,3,3,6113,3,3,3,6121,3,3,
3,3,6131,6133,3,3,3,3,6143,3,3,3,6151,3,3,3,3,3,
6163,3,3,3,3,6173,3,3,3,3,3,3,3,3,3,3,3,6197,6199,3,
6203,3,3,3,6211,3,3,6217,3,6221,3,3,3,6229,3,3,3,3,3,
3,3,3,6247,3,3,3,3,6257,3,3,6263,3,3,6269,6271,3,3,
6277,3,3,3,3,6287,3,3,3,3,3,6299,6301,3,3,3,3,6311,3,
3,6317,3,3,6323,3,3,6329,3,3,3,6337,3,3,6343,3,3,3,
3,6353,3,3,6359,6361,3,3,6367,3,3,6373,3,3,6379,3,3,
3,3,6389,3,3,3,6397,3,3,3,3,3,3,3,3,3,3,3,6421,3,3,
6427,3,3,3,3,3,3,3,3,3,3,6449,6451,3,3,3,3,3,3,3,3,
6469,3,6473,3,3,3,6481,3,3,3,3,6491,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,6521,3,3,3,6529,3,3,3,3,3,3,3,3,6547,3,
6551,6553,3,3,3,3,6563,3,3,6569,6571,3,3,6577,3,
6581,3,3,3,3,3,3,3,3,6599,3,3,3,6607,3,3,3,3,3,6619,
3,3,3,3,3,3,3,3,6637,3,3,3,3,3,3,3,6653,3,3,6659,
6661,3,3,3,3,3,6673,3,3,6679,3,3,3,3,6689,6691,3,3,
3,3,6701,6703,3,3,6709,3,3,3,3,6719,3,3,3,3,3,3,
6733,3,6737,3,3,3,3,3,3,3,3,3,3,3,6761,6763,3,3,3,3,
3,3,3,6779,6781,3,3,3,3,6791,6793,3,3,3,3,6803,3,3,
3,3,3,3,3,3,3,6823,3,6827,6829,3,6833,3,3,3,6841,3,
3,3,3,3,3,3,6857,3,3,6863,3,3,6869,6871,3,3,3,3,3,
6883,3,3,3,3,3,3,3,6899,3,3,3,6907,3,6911,3,3,6917,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,6947,6949,3,3,3,3,6959,
6961,3,3,6967,3,6971,3,3,6977,3,3,6983,3,3,3,6991,3,
3,6997,3,7001,3,3,3,3,3,7013,3,3,7019,3,3,3,7027,3,
3,3,3,3,7039,3,7043,3,3,3,3,3,3,7057,3,3,3,3,3,7069,
3,3,3,3,7079,3,3,3,3,3,3,3,3,3,3,3,7103,3,3,7109,3,3,
3,3,3,7121,3,3,7127,7129,3,3,3,3,3,3,3,3,3,3,7151,3,
3,3,7159,3,3,3,3,3,3,3,3,7177,3,3,3,3,7187,3,3,7193,
3,3,3,3,3,3,7207,3,7211,7213,3,3,7219,3,3,3,3,7229,3,
3,3,7237,3,3,7243,3,7247,3,3,7253,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,7283,3,3,3,3,3,3,7297,3,3,3,3,7307,7309,3,
3,3,3,3,7321,3,3,3,3,7331,7333,3,3,3,3,3,3,3,7349,
7351,3,3,3,3,3,3,3,3,7369,3,3,3,3,3,3,3,3,3,3,3,7393,
3,3,3,3,3,3,3,3,7411,3,3,7417,3,3,3,3,3,3,3,7433,3,3,3,
3,3,3,3,3,7451,3,3,7457,7459,3,3,3,3,3,3,3,3,7477,3,
7481,3,3,7487,7489,3,3,3,3,7499,3,3,3,7507,3,3,3,3,
7517,3,3,7523,3,3,7529,3,3,3,7537,3,7541,3,3,7547,
7549,3,3,3,3,7559,7561,3,3,3,3,3,7573,3,7577,3,3,
7583,3,3,7589,7591,3,3,3,3,3,7603,3,7607,3,3,3,3,3,
3,7621,3,3,3,3,3,3,3,3,7639,3,7643,3,3,7649,3,3,3,3,
3,3,3,3,3,7669,3,7673,3,3,3,7681,3,3,7687,3,7691,3,
3,3,7699,3,7703,3,3,3,3,3,3,7717,3,3,7723,3,7727,3,
3,3,3,3,3,7741,3,3,3,3,3,7753,3,7757,7759,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,7789,3,7793,3,3,3,3,3,3,3,3,3,3,3,
7817,3,3,7823,3,3,7829,3,3,3,3,3,7841,3,3,3,3,3,
7853,3,3,3,3,3,3,7867,3,3,7873,3,7877,7879,3,7883,3,
3,3,3,3,3,3,3,7901,3,3,7907,3,3,3,3,3,7919,3,3,3,
7927,3,3,7933,3,7937,3,3,3,3,3,7949,7951,3,3,3,3,3,
7963,3,3,3,3,3,3,3,3,3,3,3,3,3,3,7993,3,3,3,3,3,3,3,
8009,8011,3,3,8017,3,3,3,3,3,3,3,3,3,3,8039,3,3,3,3,3,
3,8053,3,3,8059,3,3,3,3,8069,3,3,3,3,3,8081,3,3,
8087,8089,3,8093,3,3,3,8101,3,3,3,3,8111,3,3,8117,3,
3,8123,3,3,3,3,3,3,3,3,3,3,3,8147,3,3,3,3,3,3,8161,3,
3,8167,3,8171,3,3,3,8179,3,3,3,3,3,8191,3,3,3,3,3,3,
3,3,8209,3,3,3,3,8219,8221,3,3,3,3,8231,8233,3,8237,
3,3,8243,3,3,3,3,3,3,3,3,3,8263,3,3,8269,3,8273,3,3,
3,3,3,3,8287,3,8291,8293,3,8297,3,3,3,3,3,3,8311,3,3,
8317,3,3,3,3,3,8329,3,3,3,3,3,3,3,3,3,3,3,8353,3,3,3,
3,8363,3,3,8369,3,3,3,8377,3,3,3,3,8387,8389,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,8419,3,8423,3,3,8429,8431,3,3,
3,3,3,8443,3,8447,3,3,3,3,3,3,8461,3,3,8467,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,8501,3,3,3,3,3,8513,3,3,3,
8521,3,3,8527,3,3,3,3,8537,8539,3,8543,3,3,3,3,3,3,
3,3,3,8563,3,3,3,3,8573,3,3,3,8581,3,3,3,3,3,3,3,
8597,8599,3,3,3,3,8609,3,3,3,3,3,3,8623,3,8627,8629,
3,3,3,3,3,8641,3,3,8647,3,3,3,3,3,3,3,8663,3,3,8669,
3,3,3,8677,3,8681,3,3,3,8689,3,8693,3,3,8699,3,3,3,
8707,3,3,8713,3,3,8719,3,3,3,3,3,8731,3,3,8737,3,
8741,3,3,8747,3,3,8753,3,3,3,8761,3,3,3,3,3,3,3,3,
8779,3,8783,3,3,3,3,3,3,3,3,3,8803,3,8807,3,3,3,3,3,
8819,8821,3,3,3,3,8831,3,3,8837,8839,3,3,3,3,8849,3,
3,3,3,3,8861,8863,3,8867,3,3,3,3,3,3,3,3,3,8887,3,3,
8893,3,3,3,3,3,3,3,3,3,3,3,3,3,3,8923,3,3,8929,3,
8933,3,3,3,8941,3,3,3,3,8951,3,3,3,3,3,8963,3,3,
8969,8971,3,3,3,3,3,3,3,3,3,3,3,3,3,8999,9001,3,3,
9007,3,9011,9013,3,3,3,3,3,3,3,9029,3,3,3,3,3,9041,
9043,3,3,9049,3,3,3,3,9059,3,3,3,9067,3,3,3,3,3,3,3,
3,3,3,3,9091,3,3,3,3,3,9103,3,3,9109,3,3,3,3,3,3,3,3,
9127,3,3,9133,3,9137,3,3,3,3,3,3,9151,3,3,9157,3,
9161,3,3,3,3,3,9173,3,3,3,9181,3,3,9187,3,3,3,3,3,
9199,3,9203,3,3,9209,3,3,3,3,3,9221,3,3,9227,3,3,3,
3,3,9239,9241,3,3,3,3,3,3,3,9257,3,3,3,3,3,3,3,3,3,
9277,3,9281,9283,3,3,3,3,9293,3,3,3,3,3,3,3,3,9311,3,
3,3,9319,3,9323,3,3,3,3,3,3,9337,3,9341,9343,3,3,
9349,3,3,3,3,3,3,3,3,3,3,9371,3,3,9377,3,3,3,3,3,3,
9391,3,3,9397,3,3,9403,3,3,3,3,9413,3,3,9419,9421,3,
3,3,3,9431,9433,3,9437,9439,3,3,3,3,3,3,3,3,3,3,
9461,9463,3,9467,3,3,9473,3,3,9479,3,3,3,3,3,9491,3,
3,9497,3,3,3,3,3,3,9511,3,3,3,3,9521,3,3,3,3,3,9533,3,
3,9539,3,3,3,9547,3,9551,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,9587,3,3,3,3,3,3,9601,3,3,3,3,3,9613,3,3,9619,
3,9623,3,3,9629,9631,3,3,3,3,3,9643,3,3,9649,3,3,3,
3,3,9661,3,3,3,3,3,3,3,9677,9679,3,3,3,3,9689,3,3,3,
9697,3,3,3,3,3,3,3,3,3,3,9719,9721,3,3,3,3,3,9733,3,
3,9739,3,9743,3,3,9749,3,3,3,3,3,3,3,3,9767,9769,3,
3,3,3,3,9781,3,3,9787,3,9791,3,3,3,3,3,9803,3,3,3,
9811,3,3,9817,3,3,3,3,3,9829,3,9833,3,3,9839,3,3,3,3,
3,9851,3,3,9857,9859,3,3,3,3,3,9871,3,3,3,3,3,9883,
3,9887,3,3,3,3,3,3,9901,3,3,9907,3,3,3,3,3,3,3,9923,
3,3,9929,9931,3,3,3,3,9941,3,3,3,9949,3,3,3,3,3,3,3,
3,9967,3,3,9973,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,10007,
10009,3,3,3,3,3,3,3,3,3,3,3,3,3,10037,10039,3,3,3,3,
3,3,3,3,3,3,10061,3,3,10067,10069,3,3,3,3,10079,3,3,
3,3,3,10091,10093,3,3,10099,3,10103,3,3,3,10111,3,
3,3,3,3,3,3,3,3,3,10133,3,3,10139,10141,3,3,3,3,
10151,3,3,3,10159,3,10163,3,3,10169,3,3,3,10177,3,
10181,3,3,3,3,3,10193,3,3,3,3,3,3,3,3,10211,3,3,3,3,3,
10223,3,3,3,3,3,3,3,3,3,10243,3,10247,3,3,10253,3,3,
10259,3,3,3,10267,3,10271,10273,3,3,3,3,3,3,3,
10289,3,3,3,3,3,10301,10303,3,3,3,3,10313,3,3,3,
10321,3,3,3,3,10331,10333,3,10337,3,3,10343,3,3,3,
3,3,3,10357,3,3,3,3,3,10369,3,3,3,3,3,3,3,3,3,3,
10391,3,3,3,10399,3,3,3,3,3,3,3,3,3,3,3,3,3,10427,
10429,3,10433,3,3,3,3,3,3,3,3,3,10453,3,10457,
10459,3,10463,3,3,3,3,3,3,10477,3,3,3,3,10487,3,3,3,
3,3,10499,10501,3,3,3,3,3,10513,3,3,3,3,3,3,3,10529,
10531,3,3,3,3,3,3,3,3,3,3,3,3,3,10559,3,3,3,10567,3,
3,3,3,3,3,3,3,3,3,10589,3,3,3,10597,3,10601,3,3,
10607,3,3,10613,3,3,3,3,3,3,10627,3,10631,3,3,3,
10639,3,3,3,3,3,10651,3,3,10657,3,3,10663,3,10667,
3,3,3,3,3,3,3,3,3,10687,3,10691,3,3,3,3,3,3,3,3,
10709,10711,3,3,3,3,3,10723,3,3,10729,3,10733,3,3,
10739,3,3,3,3,3,3,10753,3,3,3,3,3,3,3,3,10771,3,3,3,
3,10781,3,3,3,10789,3,3,3,3,10799,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,10831,3,3,10837,3,3,3,3,10847,3,3,10853,
3,3,10859,10861,3,3,10867,3,3,3,3,3,3,3,10883,3,3,
10889,10891,3,3,3,3,3,10903,3,3,10909,3,3,3,3,3,3,3,
3,3,3,3,3,3,10937,10939,3,3,3,3,10949,3,3,3,10957,3,
3,3,3,3,3,3,10973,3,3,10979,3,3,3,10987,3,3,10993,3,
3,3,3,11003,3,3,3,3,3,3,3,3,3,3,3,11027,3,3,3,3,3,3,3,
3,3,11047,3,3,3,3,11057,11059,3,3,3,3,11069,11071,3,
3,3,3,3,11083,3,11087,3,3,11093,3,3,3,3,3,3,3,3,3,
11113,3,11117,11119,3,3,3,3,3,11131,3,3,3,3,3,3,3,3,
11149,3,3,3,3,11159,11161,3,3,3,3,11171,11173,3,
11177,3,3,3,3,3,3,3,3,3,11197,3,3,3,3,3,3,3,11213,3,3,
3,3,3,3,3,3,3,3,3,3,11239,3,11243,3,3,3,11251,3,3,
11257,3,11261,3,3,3,3,3,11273,3,3,11279,3,3,3,11287,
3,3,3,3,3,11299,3,3,3,3,3,11311,3,3,11317,3,11321,3,
3,3,11329,3,3,3,3,3,3,3,3,3,3,11351,11353,3,3,3,3,3,3,
3,11369,3,3,3,3,3,3,11383,3,3,3,3,11393,3,3,11399,3,
3,3,3,3,11411,3,3,3,3,3,11423,3,3,3,3,3,3,11437,3,3,
11443,3,11447,3,3,3,3,3,3,3,3,3,11467,3,11471,3,3,3,
3,3,11483,3,3,11489,11491,3,3,11497,3,3,11503,3,3,3,
3,3,3,3,11519,3,3,3,11527,3,3,3,3,3,3,3,3,3,3,11549,
11551,3,3,3,3,3,3,3,3,3,3,3,3,3,11579,3,3,3,11587,3,3,
11593,3,11597,3,3,3,3,3,3,3,3,3,11617,3,11621,3,3,3,
3,3,11633,3,3,3,3,3,3,3,3,3,3,3,11657,3,3,3,3,3,3,3,3,
3,11677,3,11681,3,3,3,11689,3,3,3,3,11699,11701,3,3,
3,3,3,3,3,11717,11719,3,3,3,3,3,11731,3,3,3,3,3,
11743,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,11777,11779,3,
11783,3,3,11789,3,3,3,3,3,11801,3,3,11807,3,3,11813,
3,3,3,11821,3,3,11827,3,11831,11833,3,3,11839,3,3,3,
3,3,3,3,3,3,3,3,11863,3,11867,3,3,3,3,3,3,3,3,3,11887,
3,3,3,3,11897,3,3,11903,3,3,11909,3,3,3,3,3,3,11923,
3,11927,3,3,11933,3,3,11939,11941,3,3,3,3,3,11953,3,
3,11959,3,3,3,3,11969,11971,3,3,3,3,11981,3,3,11987,
3,3,3,3,3,3,3,3,3,12007,3,12011,3,3,3,3,3,3,3,3,3,3,3,
3,12037,3,12041,12043,3,3,12049,3,3,3,3,3,3,3,3,3,3,
12071,12073,3,3,3,3,3,3,3,3,3,3,3,12097,3,12101,3,3,
12107,12109,3,12113,3,3,12119,3,3,3,3,3,3,3,3,3,3,3,
12143,3,3,12149,3,3,3,12157,3,12161,12163,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,12197,3,3,12203,3,3,3,12211,3,
3,3,3,3,3,3,12227,3,3,3,3,3,12239,12241,3,3,3,3,
12251,12253,3,3,3,3,12263,3,3,12269,3,3,3,12277,3,
12281,3,3,3,12289,3,3,3,3,3,12301,3,3,3,3,3,3,3,3,3,
3,12323,3,3,12329,3,3,3,3,3,3,12343,3,12347,3,3,3,3,
3,3,3,3,3,3,3,3,12373,3,12377,12379,3,3,3,3,3,12391,
3,3,3,3,12401,3,3,3,12409,3,12413,3,3,3,12421,3,3,3,
3,3,12433,3,12437,3,3,3,3,3,3,12451,3,3,12457,3,3,3,
3,3,3,3,12473,3,3,12479,3,3,3,12487,3,12491,3,3,
12497,3,3,12503,3,3,3,12511,3,3,12517,3,3,3,3,
12527,3,3,3,3,3,12539,12541,3,3,12547,3,3,12553,3,
3,3,3,3,3,3,12569,3,3,3,12577,3,3,12583,3,3,12589,3,
3,3,3,3,12601,3,3,3,3,12611,12613,3,3,12619,3,3,3,3,
3,3,3,3,12637,3,12641,3,3,12647,3,3,12653,3,3,
12659,3,3,3,3,3,12671,3,3,3,3,3,3,3,3,12689,3,3,3,
12697,3,3,12703,3,3,3,3,12713,3,3,3,12721,3,3,3,3,3,
3,3,3,12739,3,12743,3,3,3,3,3,3,12757,3,3,12763,3,3,
3,3,3,3,3,3,12781,3,3,3,3,12791,3,3,3,12799,3,3,3,3,
12809,3,3,3,3,3,12821,12823,3,3,12829,3,3,3,3,3,
12841,3,3,3,3,3,12853,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,12889,3,12893,3,3,12899,3,3,3,12907,3,12911,3,3,
12917,12919,3,12923,3,3,3,3,3,3,3,3,12941,3,3,3,3,3,
12953,3,3,12959,3,3,3,12967,3,3,12973,3,3,12979,3,
12983,3,3,3,3,3,3,3,3,13001,13003,3,13007,13009,3,
3,3,3,3,3,3,3,3,3,3,13033,3,13037,3,3,13043,3,3,
13049,3,3,3,3,3,3,13063,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
13093,3,3,13099,3,13103,3,3,13109,3,3,3,3,3,13121,
3,3,13127,3,3,3,3,3,3,3,3,3,13147,3,13151,3,3,3,
13159,3,13163,3,3,3,13171,3,3,13177,3,3,13183,3,
13187,3,3,3,3,3,3,3,3,3,3,3,3,3,3,13217,13219,3,3,3,
3,13229,3,3,3,3,3,13241,3,3,3,13249,3,3,3,3,13259,3,
3,3,13267,3,3,3,3,3,3,3,3,3,3,3,13291,3,3,13297,3,3,
3,3,3,13309,3,13313,3,3,3,3,3,3,13327,3,13331,3,3,
13337,13339,3,3,3,3,3,3,3,3,3,3,3,3,3,13367,3,3,3,3,
3,3,13381,3,3,3,3,3,3,3,13397,13399,3,3,3,3,3,13411,
3,3,13417,3,13421,3,3,3,3,3,3,3,3,3,13441,3,3,3,3,
13451,3,3,13457,3,3,13463,3,3,13469,3,3,3,13477,3,
3,3,3,13487,3,3,3,3,3,13499,3,3,3,3,3,3,13513,3,3,3,
3,13523,3,3,3,3,3,3,13537,3,3,3,3,3,3,3,13553,3,3,3,
3,3,3,13567,3,3,3,3,13577,3,3,3,3,3,3,13591,3,3,
13597,3,3,3,3,3,3,3,13613,3,3,13619,3,3,3,13627,3,3,
13633,3,3,3,3,3,3,3,13649,3,3,3,3,3,3,3,3,3,13669,3,
3,3,3,13679,13681,3,3,13687,3,13691,13693,3,13697,
3,3,3,3,3,13709,13711,3,3,3,3,13721,13723,3,3,
13729,3,3,3,3,3,3,3,3,3,3,13751,3,3,13757,13759,3,
13763,3,3,3,3,3,3,3,3,13781,3,3,3,13789,3,3,3,3,
13799,3,3,3,13807,3,3,3,3,3,3,3,3,3,3,13829,13831,3,
3,3,3,13841,3,3,3,3,3,3,3,3,13859,3,3,3,3,3,3,13873,
3,13877,13879,3,13883,3,3,3,3,3,3,3,3,13901,13903,
3,13907,3,3,13913,3,3,3,13921,3,3,3,3,13931,13933,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,13963,3,13967,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,13997,13999,3,3,3,3,14009,14011,3,3,
3,3,3,3,3,3,14029,3,14033,3,3,3,3,3,3,3,3,14051,3,3,
14057,3,3,3,3,3,3,14071,3,3,3,3,14081,14083,3,
14087,3,3,3,3,3,3,3,3,3,14107,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,14143,3,3,14149,3,14153,3,3,14159,3,3,3,3,
3,3,14173,3,14177,3,3,3,3,3,3,3,3,3,14197,3,3,3,3,
14207,3,3,3,3,3,3,14221,3,3,3,3,3,3,3,3,3,3,14243,3,
3,14249,14251,3,3,3,3,3,3,3,3,3,3,3,3,3,3,14281,3,3,
3,3,3,14293,3,3,3,3,14303,3,3,3,3,3,3,3,3,14321,
14323,3,14327,3,3,3,3,3,3,14341,3,3,14347,3,3,3,3,3,
3,3,3,3,3,14369,3,3,3,3,3,3,3,3,14387,14389,3,3,3,3,3,
14401,3,3,14407,3,14411,3,3,3,14419,3,14423,3,3,3,
14431,3,3,14437,3,3,3,3,14447,14449,3,3,3,3,3,14461,
3,3,3,3,3,3,3,3,14479,3,3,3,3,14489,3,3,3,3,3,3,14503,
3,3,3,3,3,3,3,14519,3,3,3,3,3,3,14533,3,14537,3,3,
14543,3,3,14549,14551,3,3,14557,3,14561,14563,3,3,
3,3,3,3,3,3,3,3,3,3,3,14591,14593,3,3,3,3,3,3,3,3,3,3,3,
3,3,14621,3,3,14627,14629,3,14633,3,3,14639,3,3,3,3,
3,3,14653,3,14657,3,3,3,3,3,14669,3,3,3,3,3,3,14683,
3,3,3,3,3,3,3,14699,3,3,3,3,3,3,14713,3,14717,3,3,
14723,3,3,3,14731,3,3,14737,3,14741,3,3,14747,3,3,
14753,3,3,14759,3,3,3,14767,3,14771,3,3,3,14779,3,
14783,3,3,3,3,3,3,14797,3,3,3,3,3,3,3,14813,3,3,3,
14821,3,3,14827,3,14831,3,3,3,3,3,14843,3,3,3,14851,
3,3,3,3,3,3,3,14867,14869,3,3,3,3,14879,3,3,3,14887,
3,14891,3,3,14897,3,3,3,3,3,3,3,3,3,3,3,3,14923,3,3,
14929,3,3,3,3,14939,3,3,3,14947,3,14951,3,3,14957,3,
3,3,3,3,14969,3,3,3,3,3,3,14983,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,15013,3,15017,3,3,3,3,3,3,15031,3,3,3,3,3,3,3,3,3,
3,15053,3,3,3,15061,3,3,3,3,3,15073,3,15077,3,3,
15083,3,3,3,15091,3,3,3,3,15101,3,3,15107,3,3,3,3,3,
3,15121,3,3,3,3,15131,3,3,15137,15139,3,3,3,3,15149,
3,3,3,3,3,15161,3,3,3,3,3,15173,3,3,3,3,3,3,15187,3,3,
15193,3,3,15199,3,3,3,3,3,3,3,3,15217,3,3,3,3,15227,
3,3,15233,3,3,3,15241,3,3,3,3,3,3,3,3,15259,3,15263,
3,3,15269,15271,3,3,15277,3,3,3,3,15287,15289,3,3,3,
3,15299,3,3,3,15307,3,3,15313,3,3,15319,3,3,3,3,
15329,15331,3,3,3,3,3,3,3,3,15349,3,3,3,3,15359,
15361,3,3,3,3,3,15373,3,15377,3,3,15383,3,3,3,15391,
3,3,3,3,15401,3,3,3,3,3,15413,3,3,3,3,3,3,15427,3,3,3,
3,3,15439,3,15443,3,3,3,15451,3,3,3,3,15461,3,3,
15467,3,3,15473,3,3,3,3,3,3,3,3,3,15493,3,15497,3,3,
3,3,3,3,15511,3,3,3,3,3,3,3,15527,3,3,3,3,3,3,15541,3,
3,3,3,15551,3,3,3,15559,3,3,3,3,15569,3,3,3,3,3,
15581,15583,3,3,3,3,3,3,3,3,15601,3,3,15607,3,3,3,3,
3,15619,3,3,3,3,15629,3,3,3,3,3,15641,15643,3,15647,
15649,3,3,3,3,3,15661,3,3,15667,3,15671,3,3,3,15679,
3,15683,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,15727,
3,15731,15733,3,15737,15739,3,3,3,3,15749,3,3,3,3,3,
15761,3,3,15767,3,3,15773,3,3,3,3,3,3,15787,3,15791,
3,3,15797,3,3,15803,3,3,15809,3,3,3,15817,3,3,15823,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,15859,3,3,3,3,3,3,3,3,
15877,3,15881,3,3,15887,15889,3,3,3,3,3,15901,3,3,
15907,3,3,15913,3,3,15919,3,15923,3,3,3,3,3,3,15937,
3,3,3,3,3,3,3,3,3,3,15959,3,3,3,3,3,15971,15973,3,3,3,
3,3,3,3,3,15991,3,3,3,3,16001,3,3,16007,3,3,3,3,3,3,3,
3,3,3,3,3,16033,3,3,3,3,3,3,3,3,3,3,3,16057,3,16061,
16063,3,16067,16069,3,16073,3,3,3,3,3,3,16087,3,
16091,3,3,16097,3,3,16103,3,3,3,16111,3,3,3,3,3,3,3,
16127,3,3,3,3,3,16139,16141,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,16183,3,16187,16189,3,16193,3,3,3,3,3,
3,3,3,3,3,3,16217,3,3,16223,3,3,16229,16231,3,3,3,3,
3,3,3,3,16249,3,16253,3,3,3,3,3,3,16267,3,3,16273,3,
3,3,3,3,3,3,3,3,3,3,3,3,16301,3,3,3,3,3,3,3,3,16319,3,3,
3,3,3,3,16333,3,3,16339,3,3,3,3,16349,3,3,3,3,3,
16361,16363,3,3,16369,3,3,3,3,3,16381,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,16411,3,3,16417,3,16421,3,3,16427,3,3,
16433,3,3,3,3,3,3,16447,3,16451,16453,3,3,3,3,3,3,3,
3,3,3,3,16477,3,16481,3,3,16487,3,3,16493,3,3,3,3,3,
3,3,3,3,3,3,3,16519,3,3,3,3,16529,3,3,3,3,3,3,3,3,
16547,3,3,16553,3,3,3,16561,3,3,16567,3,3,16573,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,16603,3,16607,3,3,3,3,3,16619,
3,3,3,3,3,16631,16633,3,3,3,3,3,3,3,16649,16651,3,3,
16657,3,16661,3,3,3,3,3,16673,3,3,3,3,3,3,3,3,16691,
16693,3,3,16699,3,16703,3,3,3,3,3,3,3,3,3,3,3,3,
16729,3,3,3,3,3,16741,3,3,16747,3,3,3,3,3,16759,3,
16763,3,3,3,3,3,3,3,3,3,3,3,16787,3,3,3,3,3,3,3,3,3,3,3,
16811,3,3,3,3,3,16823,3,3,16829,16831,3,3,3,3,3,
16843,3,3,3,3,3,3,3,3,3,3,3,3,3,16871,3,3,3,16879,3,
16883,3,3,16889,3,3,3,3,3,16901,16903,3,3,3,3,3,3,3,
3,16921,3,3,16927,3,16931,3,3,16937,3,3,16943,3,3,3,
3,3,3,3,3,3,16963,3,3,3,3,3,3,3,16979,16981,3,3,
16987,3,3,16993,3,3,3,3,3,3,3,3,17011,3,3,3,3,17021,3,
3,17027,17029,3,17033,3,3,3,17041,3,3,17047,3,3,
17053,3,3,3,3,3,3,3,3,3,3,3,17077,3,3,3,3,3,3,3,17093,
3,3,17099,3,3,3,17107,3,3,3,3,17117,3,3,17123,3,3,3,3,
3,3,17137,3,3,3,3,3,3,3,3,3,3,17159,3,3,3,17167,3,3,3,
3,3,3,3,17183,3,3,17189,17191,3,3,3,3,3,17203,3,
17207,17209,3,3,3,3,3,3,3,3,3,3,17231,3,3,3,17239,3,
3,3,3,3,3,3,3,17257,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
17291,17293,3,3,17299,3,3,3,3,3,3,3,3,17317,3,17321,
3,3,17327,3,3,17333,3,3,3,17341,3,3,3,3,17351,3,3,3,
17359,3,3,3,3,3,3,3,3,17377,3,3,17383,3,17387,17389,
3,17393,3,3,3,17401,3,3,3,3,3,3,3,17417,17419,3,3,3,
3,3,17431,3,3,3,3,3,17443,3,3,17449,3,3,3,3,3,3,3,3,
17467,3,17471,3,3,17477,3,3,17483,3,3,17489,17491,
3,3,17497,3,3,3,3,3,17509,3,3,3,3,17519,3,3,3,3,3,3,3,
3,3,17539,3,3,3,3,3,17551,3,3,3,3,3,3,3,3,17569,3,
17573,3,3,17579,17581,3,3,3,3,3,3,3,17597,17599,3,3,
3,3,17609,3,3,3,3,3,3,17623,3,17627,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,17657,17659,3,3,3,3,17669,3,3,3,3,3,17681,
17683,3,3,3,3,3,3,3,3,3,3,3,17707,3,3,17713,3,3,3,3,3,
3,3,17729,3,3,3,17737,3,3,3,3,17747,17749,3,3,3,3,3,
17761,3,3,3,3,3,3,3,3,3,3,17783,3,3,17789,17791,3,3,
3,3,3,3,3,17807,3,3,3,3,3,3,3,3,3,17827,3,3,3,3,17837,
17839,3,3,3,3,3,17851,3,3,3,3,3,17863,3,3,3,3,3,3,3,3,
17881,3,3,3,3,17891,3,3,3,3,3,17903,3,3,17909,17911,
3,3,3,3,17921,17923,3,3,17929,3,3,3,3,17939,3,3,3,3,
3,3,3,3,17957,17959,3,3,3,3,3,17971,3,3,17977,3,
17981,3,3,17987,17989,3,3,3,3,3,3,3,3,3,3,3,18013,3,
3,3,3,3,3,3,3,3,3,3,3,3,18041,18043,3,18047,18049,3,
3,3,3,18059,18061,3,3,3,3,3,3,3,18077,3,3,3,3,3,
18089,3,3,3,18097,3,3,3,3,3,3,3,3,3,3,18119,18121,3,3,
18127,3,18131,18133,3,3,3,3,18143,3,3,18149,3,3,3,3,
3,3,3,3,3,18169,3,3,3,3,3,18181,3,3,3,3,18191,3,3,3,
18199,3,3,3,3,3,18211,3,3,18217,3,3,18223,3,3,18229,
3,18233,3,3,3,3,3,3,3,3,18251,18253,3,18257,3,3,3,3,
3,18269,3,3,3,3,3,3,3,3,18287,18289,3,3,3,3,3,18301,
3,3,18307,3,18311,18313,3,3,3,3,3,3,3,18329,3,3,3,3,3,
18341,3,3,3,3,3,18353,3,3,3,3,3,3,18367,3,18371,3,3,
3,18379,3,3,3,3,3,3,3,3,18397,3,18401,3,3,3,3,3,
18413,3,3,3,3,3,3,18427,3,3,18433,3,3,18439,3,18443,
3,3,3,18451,3,3,18457,3,18461,3,3,3,3,3,3,3,3,3,
18481,3,3,3,3,3,18493,3,3,3,3,18503,3,3,3,3,3,3,
18517,3,18521,18523,3,3,3,3,3,3,3,18539,18541,3,3,3,
3,3,18553,3,3,3,3,3,3,3,3,3,3,3,3,3,3,18583,3,18587,3,
3,18593,3,3,3,3,3,3,3,3,3,3,3,18617,3,3,3,3,3,3,3,3,3,
18637,3,3,3,3,3,3,3,3,3,3,3,18661,3,3,3,3,18671,3,3,3,
18679,3,3,3,3,3,18691,3,3,3,3,18701,3,3,3,3,3,18713,
3,3,18719,3,3,3,3,3,18731,3,3,3,3,3,18743,3,3,18749,
3,3,3,18757,3,3,3,3,3,3,3,18773,3,3,3,3,3,3,18787,3,3,
18793,3,18797,3,3,18803,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,18839,3,3,3,3,3,3,3,3,3,18859,3,3,3,3,18869,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,18899,3,3,3,3,3,18911,18913,3,
18917,18919,3,3,3,3,3,3,3,3,3,3,3,3,3,18947,3,3,3,3,3,
18959,3,3,3,3,3,3,18973,3,3,18979,3,3,3,3,3,3,3,3,3,3,
19001,3,3,3,19009,3,19013,3,3,3,3,3,3,3,3,19031,3,3,
19037,3,3,3,3,3,3,19051,3,3,3,3,3,3,3,3,19069,3,
19073,3,3,19079,19081,3,3,19087,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,19121,3,3,3,3,3,3,3,3,19139,19141,3,3,3,3,
3,3,3,19157,3,3,19163,3,3,3,3,3,3,3,3,19181,19183,3,
3,3,3,3,3,3,3,3,3,3,19207,3,19211,19213,3,3,19219,3,3,
3,3,3,19231,3,3,19237,3,3,3,3,3,19249,3,3,3,3,19259,
3,3,3,19267,3,3,19273,3,3,3,3,3,3,3,19289,3,3,3,3,3,
19301,3,3,3,19309,3,3,3,3,19319,3,3,3,3,3,3,19333,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,19373,3,3,19379,
19381,3,3,19387,3,19391,3,3,3,3,3,19403,3,3,3,3,3,3,
19417,3,19421,19423,3,19427,19429,3,19433,3,3,3,
19441,3,3,19447,3,3,3,3,19457,3,3,19463,3,3,19469,
19471,3,3,19477,3,3,19483,3,3,19489,3,3,3,3,3,19501,
3,3,19507,3,3,3,3,3,3,3,3,3,3,3,19531,3,3,3,3,19541,
19543,3,3,3,3,19553,3,3,19559,3,3,3,3,3,19571,3,3,
19577,3,3,19583,3,3,3,3,3,3,19597,3,3,19603,3,3,
19609,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
19661,3,3,3,3,3,3,3,3,3,19681,3,3,19687,3,3,3,3,
19697,19699,3,3,3,3,19709,3,3,3,19717,3,3,3,3,19727,
3,3,3,3,3,19739,3,3,3,3,3,19751,19753,3,3,19759,3,
19763,3,3,3,3,3,3,19777,3,3,3,3,3,3,3,19793,3,3,3,
19801,3,3,3,3,3,19813,3,3,19819,3,3,3,3,3,3,3,3,3,3,
19841,19843,3,3,3,3,19853,3,3,3,19861,3,3,19867,3,3,
3,3,3,3,3,3,3,3,19889,19891,3,3,3,3,3,3,3,3,3,3,19913,
3,3,19919,3,3,3,19927,3,3,3,3,19937,3,3,3,3,3,19949,
3,3,3,3,3,19961,19963,3,3,3,3,19973,3,3,19979,3,3,3,
3,3,19991,19993,3,19997,3,3,3,3,3,3,20011,3,3,3,3,
20021,20023,3,3,20029,3,3,3,3,3,3,3,3,20047,3,20051,
3,3,3,3,3,20063,3,3,3,20071,3,3,3,3,3,3,3,3,20089,3,3,
3,3,3,20101,3,3,20107,3,3,20113,3,20117,3,3,20123,3,
3,20129,3,3,3,3,3,3,20143,3,20147,20149,3,3,3,3,3,
20161,3,3,3,3,3,20173,3,20177,3,3,20183,3,3,3,3,3,3,
3,3,20201,3,3,3,3,3,3,3,3,20219,3,3,3,3,3,20231,
20233,3,3,3,3,3,3,3,20249,3,3,3,3,3,20261,3,3,3,
20269,3,3,3,3,3,3,3,3,20287,3,3,3,3,20297,3,3,3,3,3,3,
3,3,3,3,3,3,20323,3,20327,3,3,20333,3,3,3,20341,3,3,
20347,3,3,20353,3,20357,20359,3,3,3,3,20369,3,3,3,3,
3,3,3,3,3,20389,3,20393,3,3,20399,3,3,3,20407,3,
20411,3,3,3,3,3,3,3,3,3,20431,3,3,3,3,20441,20443,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,20477,20479,3,20483,3,3,3,
3,3,3,3,3,3,3,3,20507,20509,3,3,3,3,3,20521,3,3,3,3,3,
20533,3,3,3,3,20543,3,3,20549,20551,3,3,3,3,3,20563,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,20593,3,3,20599,3,3,3,3,3,
20611,3,3,3,3,3,3,3,20627,3,3,3,3,3,20639,20641,3,3,3,
3,3,3,3,3,3,3,20663,3,3,3,3,3,3,3,3,20681,3,3,3,3,3,
20693,3,3,3,3,3,3,20707,3,3,3,3,20717,20719,3,3,3,3,
3,20731,3,3,3,3,3,20743,3,20747,20749,3,20753,3,3,
20759,3,3,3,3,3,20771,20773,3,3,3,3,3,3,3,20789,3,3,
3,3,3,3,3,3,20807,20809,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,20849,3,3,3,20857,3,3,3,3,3,3,3,20873,3,3,
20879,3,3,3,20887,3,3,3,3,20897,20899,3,20903,3,3,3,
3,3,3,3,3,20921,3,3,3,20929,3,3,3,3,20939,3,3,3,
20947,3,3,3,3,3,20959,3,20963,3,3,3,3,3,3,3,3,20981,
20983,3,3,3,3,3,3,3,3,21001,3,3,3,3,21011,21013,3,
21017,21019,3,21023,3,3,3,21031,3,3,3,3,3,3,3,3,3,3,
3,3,3,21059,21061,3,3,21067,3,3,3,3,3,3,3,3,3,3,
21089,3,3,3,3,3,21101,3,3,21107,3,3,3,3,3,3,21121,3,3,
3,3,3,3,3,3,21139,3,21143,3,3,21149,3,3,3,21157,3,3,
21163,3,3,21169,3,3,3,3,21179,3,3,3,21187,3,21191,
21193,3,3,3,3,3,3,3,3,21211,3,3,3,3,21221,3,3,21227,3,
3,3,3,3,3,3,3,3,21247,3,3,3,3,3,3,3,3,3,3,21269,3,3,3,
21277,3,3,21283,3,3,3,3,3,3,3,3,3,3,3,3,3,3,21313,3,
21317,21319,3,21323,3,3,3,3,3,3,3,3,21341,3,3,21347,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,21377,21379,3,21383,3,3,3,
21391,3,3,21397,3,21401,3,3,21407,3,3,3,3,3,21419,3,
3,3,3,3,3,21433,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,21467,3,
3,3,3,3,3,21481,3,3,21487,3,21491,21493,3,3,21499,3,
21503,3,3,3,3,3,3,21517,3,21521,21523,3,3,21529,3,3,
3,3,3,3,3,3,3,3,3,3,3,21557,21559,3,21563,3,3,21569,
3,3,3,21577,3,3,3,3,21587,21589,3,3,3,3,21599,21601,
3,3,3,3,21611,21613,3,21617,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,21647,21649,3,3,3,3,3,21661,3,3,3,3,3,21673,3,3,3,
3,21683,3,3,3,3,3,3,3,3,21701,3,3,3,3,3,21713,3,3,3,3,
3,3,21727,3,3,3,3,21737,21739,3,3,3,3,3,21751,3,3,
21757,3,3,3,3,21767,3,3,21773,3,3,3,3,3,3,21787,3,3,
3,3,3,21799,3,21803,3,3,3,3,3,3,21817,3,21821,3,3,3,
3,3,3,3,3,21839,21841,3,3,3,3,21851,3,3,3,21859,3,
21863,3,3,3,21871,3,3,3,3,21881,3,3,3,3,3,21893,3,3,
3,3,3,3,3,3,21911,3,3,3,3,3,3,3,3,21929,3,3,3,21937,3,
3,21943,3,3,3,3,3,3,3,3,21961,3,3,3,3,3,3,3,21977,3,3,
3,3,3,3,21991,3,3,21997,3,3,22003,3,3,3,3,22013,3,3,
3,3,3,3,22027,3,22031,3,3,22037,22039,3,3,3,3,3,
22051,3,3,3,3,3,22063,3,22067,3,3,22073,3,3,22079,3,
3,3,3,3,22091,22093,3,3,3,3,3,3,3,22109,22111,3,3,3,3,
3,22123,3,3,22129,3,22133,3,3,3,3,3,3,22147,3,3,
22153,3,22157,22159,3,3,3,3,3,22171,3,3,3,3,3,3,3,3,
22189,3,22193,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22229,
3,3,3,3,3,3,3,3,22247,3,3,3,3,3,22259,3,3,3,3,3,22271,
22273,3,22277,22279,3,22283,3,3,3,22291,3,3,3,3,3,
22303,3,22307,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22343,
3,3,22349,3,3,3,3,3,3,3,3,22367,22369,3,3,3,3,3,
22381,3,3,3,3,22391,3,3,22397,3,3,3,3,3,22409,3,3,3,
3,3,3,3,3,3,3,3,22433,3,3,3,22441,3,3,22447,3,3,
22453,3,3,3,3,3,3,3,22469,3,3,3,3,3,22481,22483,3,3,
3,3,3,3,3,3,22501,3,3,3,3,22511,3,3,3,3,3,3,3,3,3,
22531,3,3,3,3,22541,22543,3,3,22549,3,3,3,3,3,3,3,3,
22567,3,22571,22573,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,22613,3,3,22619,22621,3,3,3,3,3,3,3,22637,22639,
3,22643,3,3,3,22651,3,3,3,3,3,3,3,3,22669,3,3,3,3,
22679,3,3,3,3,3,22691,3,3,22697,22699,3,3,3,3,22709,
3,3,3,22717,3,22721,3,3,22727,3,3,3,3,3,22739,22741,
3,3,3,3,22751,3,3,3,3,3,3,3,3,22769,3,3,3,22777,3,3,
22783,3,22787,3,3,3,3,3,3,3,3,3,22807,3,22811,3,3,
22817,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22853,3,3,
22859,22861,3,3,3,3,22871,3,3,22877,3,3,3,3,3,3,3,3,
3,3,3,22901,3,3,22907,3,3,3,3,3,3,22921,3,3,3,3,3,3,3,
22937,3,3,22943,3,3,3,3,3,3,3,3,22961,22963,3,3,3,3,
22973,3,3,3,3,3,3,3,3,3,22993,3,3,3,3,23003,3,3,3,
23011,3,3,23017,3,23021,3,3,23027,23029,3,3,3,3,
23039,23041,3,3,3,3,3,23053,3,23057,23059,3,23063,
3,3,3,23071,3,3,3,3,23081,3,3,23087,3,3,3,3,3,23099,
3,3,3,3,3,3,3,3,23117,3,3,3,3,3,3,23131,3,3,3,3,3,
23143,3,3,3,3,3,3,3,23159,3,3,3,23167,3,3,23173,3,3,
3,3,3,3,3,23189,3,3,3,23197,3,23201,23203,3,3,23209,
3,3,3,3,3,3,3,3,23227,3,3,3,3,3,3,3,3,3,3,3,23251,3,3,3,
3,3,3,3,3,23269,3,3,3,3,23279,3,3,3,3,3,23291,23293,
3,23297,3,3,3,3,3,3,23311,3,3,3,3,23321,3,3,23327,3,3,
23333,3,3,23339,3,3,3,3,3,3,3,3,23357,3,3,3,3,3,
23369,23371,3,3,3,3,3,3,3,3,3,3,3,3,3,23399,3,3,3,3,3,
3,3,3,23417,3,3,3,3,3,3,23431,3,3,3,3,3,3,3,23447,3,3,
3,3,3,23459,3,3,3,3,3,3,23473,3,3,3,3,3,3,3,3,3,3,3,
23497,3,3,3,3,3,23509,3,3,3,3,3,3,3,3,3,3,23531,3,3,
23537,23539,3,3,3,3,23549,3,3,3,23557,3,23561,
23563,3,23567,3,3,3,3,3,3,23581,3,3,3,3,3,23593,3,3,
23599,3,23603,3,3,23609,3,3,3,3,3,3,23623,3,23627,
23629,3,23633,3,3,3,3,3,3,3,3,3,3,3,3,3,3,23663,3,3,
23669,23671,3,3,23677,3,3,3,3,23687,23689,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,23719,3,3,3,3,3,3,3,3,3,3,23741,
23743,3,23747,3,3,23753,3,3,3,23761,3,3,23767,3,3,
23773,3,3,3,3,3,3,3,23789,3,3,3,3,3,23801,3,3,3,3,3,
23813,3,3,23819,3,3,3,23827,3,23831,23833,3,3,3,3,3,
3,3,3,3,3,3,23857,3,3,3,3,3,23869,3,23873,3,3,23879,
3,3,3,23887,3,3,23893,3,3,23899,3,3,3,3,23909,23911,
3,3,23917,3,3,3,3,3,23929,3,3,3,3,3,3,3,3,3,3,3,3,3,
23957,3,3,3,3,3,3,23971,3,3,23977,3,23981,3,3,3,3,3,
23993,3,3,3,24001,3,3,24007,3,3,3,3,3,24019,3,24023,
3,3,24029,3,3,3,3,3,3,24043,3,3,24049,3,3,3,3,3,
24061,3,3,3,3,24071,3,3,24077,3,3,24083,3,3,3,24091,
3,3,24097,3,3,24103,3,24107,24109,3,24113,3,3,3,
24121,3,3,3,3,3,24133,3,24137,3,3,3,3,3,3,24151,3,3,
3,3,3,3,3,3,24169,3,3,3,3,24179,24181,3,3,3,3,3,3,3,
24197,3,3,24203,3,3,3,3,3,3,3,3,3,24223,3,3,24229,3,
3,3,3,24239,3,3,3,24247,3,24251,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,24281,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,24317,3,3,
3,3,3,24329,3,3,3,24337,3,3,3,3,3,3,3,3,3,3,24359,3,3,
3,3,3,24371,24373,3,3,24379,3,3,3,3,3,24391,3,3,3,3,
3,3,3,24407,3,3,24413,3,3,24419,24421,3,3,3,3,3,3,3,
3,24439,3,24443,3,3,3,3,3,3,3,3,3,3,3,3,24469,3,
24473,3,3,3,24481,3,3,3,3,3,3,3,3,24499,3,3,3,3,
24509,3,3,3,24517,3,3,3,3,24527,3,3,24533,3,3,3,3,3,
3,24547,3,24551,3,3,3,3,3,3,3,3,3,24571,3,3,3,3,3,3,3,
3,3,3,24593,3,3,3,3,3,3,3,3,24611,3,3,3,3,3,24623,3,3,
3,24631,3,3,3,3,3,3,3,3,3,3,3,3,3,24659,3,3,3,3,3,
24671,3,3,24677,3,3,24683,3,3,3,24691,3,3,24697,3,3,
3,3,3,24709,3,3,3,3,3,3,3,3,3,3,3,24733,3,3,3,3,3,3,3,
24749,3,3,3,3,3,3,24763,3,24767,3,3,3,3,3,3,24781,3,
3,3,3,3,24793,3,3,24799,3,3,3,3,24809,3,3,3,3,3,
24821,3,3,3,3,3,3,3,3,3,24841,3,3,24847,3,24851,3,3,
3,24859,3,3,3,3,3,3,3,3,24877,3,3,3,3,3,24889,3,3,3,3,
3,3,3,3,24907,3,3,3,3,24917,24919,3,24923,3,3,3,3,3,
3,3,3,3,24943,3,3,3,3,24953,3,3,3,3,3,3,24967,3,
24971,3,3,24977,24979,3,3,3,3,24989,3,3,3,3,3,3,3,3,
3,3,3,25013,3,3,3,3,3,3,3,3,25031,25033,3,25037,3,3,
3,3,3,3,3,3,3,25057,3,3,3,3,3,3,3,25073,3,3,3,3,3,3,
25087,3,3,3,3,25097,3,3,3,3,3,3,25111,3,3,25117,3,
25121,3,3,25127,3,3,3,3,3,3,3,3,3,25147,3,3,25153,3,
3,3,3,25163,3,3,25169,25171,3,3,3,3,3,25183,3,3,
25189,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25219,3,3,3,3,25229,
3,3,3,25237,3,3,25243,3,25247,3,3,25253,3,3,3,25261,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25301,25303,3,
25307,25309,3,3,3,3,3,25321,3,3,3,3,3,3,3,3,25339,3,
25343,3,3,25349,3,3,3,25357,3,3,3,3,25367,3,3,
25373,3,3,3,3,3,3,3,3,25391,3,3,3,3,3,3,3,3,25409,
25411,3,3,3,3,3,25423,3,3,3,3,3,3,3,25439,3,3,3,25447,
3,3,25453,3,25457,3,3,25463,3,3,25469,25471,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25523,3,3,3,3,3,
3,25537,3,25541,3,3,3,3,3,3,3,3,3,25561,3,3,3,3,3,3,3,
25577,25579,3,25583,3,3,25589,3,3,3,3,3,25601,
25603,3,3,25609,3,3,3,3,3,25621,3,3,3,3,3,25633,3,3,
25639,3,25643,3,3,3,3,3,3,25657,3,3,3,3,25667,3,3,
25673,3,3,25679,3,3,3,3,3,3,25693,3,3,3,3,25703,3,3,
3,3,3,3,25717,3,3,3,3,3,3,3,25733,3,3,3,25741,3,3,
25747,3,3,3,3,3,25759,3,25763,3,3,3,25771,3,3,3,3,3,
3,3,3,3,3,25793,3,3,25799,25801,3,3,3,3,3,3,3,3,
25819,3,3,3,3,3,3,3,3,3,3,25841,3,3,25847,25849,3,3,
3,3,3,3,3,3,25867,3,3,25873,3,3,3,3,3,3,3,25889,3,3,3,
3,3,3,25903,3,3,3,3,25913,3,3,25919,3,3,3,3,3,25931,
25933,3,3,25939,3,25943,3,3,3,25951,3,3,3,3,3,3,3,3,
25969,3,3,3,3,3,25981,3,3,3,3,3,3,3,25997,25999,3,
26003,3,3,3,3,3,3,26017,3,26021,3,3,3,26029,3,3,3,3,
3,26041,3,3,3,3,3,26053,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
26083,3,3,3,3,3,3,3,26099,3,3,3,26107,3,26111,26113,
3,3,26119,3,3,3,3,3,3,3,3,3,3,26141,3,3,3,3,3,26153,3,
3,3,26161,3,3,3,3,26171,3,3,26177,3,3,26183,3,3,
26189,3,3,3,3,3,3,26203,3,3,26209,3,3,3,3,3,3,3,3,
26227,3,3,3,3,26237,3,3,3,3,3,26249,26251,3,3,3,3,
26261,26263,3,26267,3,3,3,3,3,3,3,3,3,3,3,3,26293,3,
26297,3,3,3,3,3,26309,3,3,3,26317,3,26321,3,3,3,3,3,
3,3,3,26339,3,3,3,26347,3,3,3,3,26357,3,3,3,3,3,3,
26371,3,3,3,3,3,3,3,26387,3,3,26393,3,3,26399,3,3,3,
26407,3,3,3,3,26417,3,3,26423,3,3,3,26431,3,3,26437,
3,3,3,3,3,26449,3,3,3,3,26459,3,3,3,3,3,3,3,3,3,26479,
3,3,3,3,26489,3,3,3,26497,3,26501,3,3,3,3,3,26513,3,
3,3,3,3,3,3,3,3,3,3,3,26539,3,3,3,3,3,3,3,3,26557,3,
26561,3,3,3,3,3,26573,3,3,3,3,3,3,3,3,26591,3,3,
26597,3,3,3,3,3,3,3,3,3,3,3,3,3,3,26627,3,3,26633,3,3,
3,26641,3,3,26647,3,3,3,3,3,3,3,3,3,3,26669,3,3,3,3,3,
26681,26683,3,26687,3,3,26693,3,3,26699,26701,3,3,
3,3,26711,26713,3,26717,3,3,26723,3,3,26729,26731,
3,3,26737,3,3,3,3,3,3,3,3,3,3,26759,3,3,3,3,3,3,3,3,
26777,3,3,26783,3,3,3,3,3,3,3,3,26801,3,3,3,3,3,
26813,3,3,3,26821,3,3,3,3,3,26833,3,3,26839,3,3,3,3,
26849,3,3,3,3,3,26861,26863,3,3,3,3,3,3,3,26879,
26881,3,3,3,3,26891,26893,3,3,3,3,26903,3,3,3,3,3,3,
3,3,26921,3,3,26927,3,3,3,3,3,3,3,3,3,26947,3,26951,
26953,3,3,26959,3,3,3,3,3,3,3,3,3,3,26981,3,3,26987,
3,3,26993,3,3,3,3,3,3,3,3,27011,3,3,27017,3,3,3,3,3,3,
27031,3,3,3,3,3,27043,3,3,3,3,3,3,3,27059,27061,3,3,
27067,3,3,27073,3,27077,3,3,3,3,3,3,27091,3,3,3,3,3,
27103,3,27107,27109,3,3,3,3,3,3,3,3,27127,3,3,3,3,3,
3,3,27143,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27179,3,3,3,
3,3,27191,3,3,27197,3,3,3,3,3,3,27211,3,3,3,3,3,3,3,3,
3,3,3,3,3,27239,27241,3,3,3,3,3,27253,3,3,27259,3,3,
3,3,3,27271,3,3,27277,3,27281,27283,3,3,3,3,3,3,3,
27299,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27329,3,3,3,27337,3,
3,3,3,3,3,3,3,3,3,3,27361,3,3,27367,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,27397,3,3,3,3,27407,27409,3,3,3,3,3,3,3,3,
27427,3,27431,3,3,27437,3,3,3,3,3,27449,3,3,3,27457,
3,3,3,3,3,3,3,3,3,3,27479,27481,3,3,27487,3,3,3,3,3,3,
3,3,3,3,27509,3,3,3,3,3,3,3,3,27527,27529,3,3,3,3,
27539,27541,3,3,3,3,27551,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
27581,27583,3,3,3,3,3,3,3,3,3,3,3,3,3,27611,3,3,27617,
3,3,3,3,3,3,27631,3,3,3,3,3,3,3,27647,3,3,27653,3,3,3,
3,3,3,3,3,3,27673,3,3,3,3,3,3,3,27689,27691,3,3,
27697,3,27701,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27733,3,
27737,27739,3,27743,3,3,27749,27751,3,3,3,3,3,
27763,3,27767,3,3,27773,3,3,27779,3,3,3,3,3,27791,
27793,3,3,27799,3,27803,3,3,27809,3,3,3,27817,3,3,
27823,3,27827,3,3,3,3,3,3,3,3,3,27847,3,27851,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,27883,3,3,3,3,27893,3,3,3,
27901,3,3,3,3,3,3,3,27917,27919,3,3,3,3,3,3,3,3,3,3,
27941,27943,3,27947,3,3,27953,3,3,3,27961,3,3,
27967,3,3,3,3,3,3,3,27983,3,3,3,3,3,3,27997,3,28001,
3,3,3,3,3,3,3,3,28019,3,3,3,28027,3,28031,3,3,3,3,3,3,
3,3,3,28051,3,3,28057,3,3,3,3,3,28069,3,3,3,3,3,
28081,3,3,28087,3,3,3,3,28097,28099,3,3,3,3,28109,
28111,3,3,3,3,3,28123,3,3,3,3,3,3,3,3,3,3,3,3,3,28151,
3,3,3,3,3,28163,3,3,3,3,3,3,3,3,28181,28183,3,3,3,3,3,
3,3,3,28201,3,3,3,3,28211,3,3,3,28219,3,3,3,3,28229,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28277,28279,
3,28283,3,3,28289,3,3,3,28297,3,3,3,3,28307,28309,3,
3,3,3,28319,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28349,28351,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28387,3,3,28393,3,3,3,3,
28403,3,3,28409,28411,3,3,3,3,3,3,3,3,28429,3,28433,
3,3,28439,3,3,3,28447,3,3,3,3,3,3,3,28463,3,3,3,3,3,3,
28477,3,3,3,3,3,3,3,28493,3,3,28499,3,3,3,3,3,3,
28513,3,28517,3,3,3,3,3,3,3,3,3,28537,3,28541,3,3,
28547,28549,3,3,3,3,28559,3,3,3,3,3,28571,28573,3,3,
28579,3,3,3,3,3,28591,3,3,28597,3,3,28603,3,28607,3,
3,3,3,3,28619,28621,3,3,28627,3,28631,3,3,3,3,3,
28643,3,3,28649,3,3,3,28657,3,28661,28663,3,3,
28669,3,3,3,3,3,3,3,3,28687,3,3,3,3,28697,3,3,28703,
3,3,3,28711,3,3,3,3,3,28723,3,3,28729,3,3,3,3,3,3,3,3,
3,3,28751,28753,3,3,28759,3,3,3,3,3,28771,3,3,3,3,3,
3,3,3,28789,3,28793,3,3,3,3,3,3,28807,3,3,28813,3,
28817,3,3,3,3,3,3,3,3,3,28837,3,3,28843,3,3,3,3,3,3,3,
28859,3,3,3,28867,3,28871,3,3,3,28879,3,3,3,3,3,3,3,
3,3,3,28901,3,3,3,28909,3,3,3,3,3,28921,3,3,28927,3,
3,28933,3,3,3,3,3,3,3,28949,3,3,3,3,3,28961,3,3,3,3,3,
3,3,3,28979,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29009,3,3,3,
29017,3,29021,29023,3,29027,3,3,29033,3,3,3,3,3,3,3,
3,3,3,3,3,29059,3,29063,3,3,3,3,3,3,29077,3,3,3,3,3,3,
3,3,3,3,3,29101,3,3,3,3,3,3,3,3,3,3,29123,3,3,29129,
29131,3,3,29137,3,3,3,3,29147,3,3,29153,3,3,3,3,3,3,
29167,3,3,29173,3,3,29179,3,3,3,3,3,29191,3,3,3,3,
29201,3,3,29207,29209,3,3,3,3,3,29221,3,3,3,3,29231,
3,3,3,3,3,29243,3,3,3,29251,3,3,3,3,3,3,3,3,29269,3,3,
3,3,3,3,3,3,29287,3,3,3,3,29297,3,3,29303,3,3,3,29311,
3,3,3,3,3,3,3,29327,3,3,29333,3,3,29339,3,3,3,29347,
3,3,3,3,3,3,3,29363,3,3,3,3,3,3,3,3,3,29383,3,29387,
29389,3,3,3,3,29399,29401,3,3,3,3,29411,3,3,3,3,3,
29423,3,3,29429,3,3,3,29437,3,3,29443,3,3,3,3,29453,
3,3,3,3,3,3,3,3,3,29473,3,3,3,3,29483,3,3,3,3,3,3,3,3,
29501,3,3,3,3,3,3,3,3,3,3,3,3,29527,3,29531,3,3,
29537,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29567,29569,3,
29573,3,3,3,29581,3,3,29587,3,3,3,3,3,29599,3,3,3,3,
3,29611,3,3,3,3,3,3,3,3,29629,3,29633,3,3,3,29641,3,3,
3,3,3,3,3,3,3,3,29663,3,3,29669,29671,3,3,3,3,3,
29683,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29717,3,3,29723,
3,3,3,3,3,3,3,3,29741,3,3,3,3,3,29753,3,3,29759,
29761,3,3,3,3,3,3,3,3,3,3,3,3,3,29789,3,3,3,3,3,3,
29803,3,3,3,3,3,3,3,29819,3,3,3,3,3,3,29833,3,29837,
3,3,3,3,3,3,29851,3,3,3,3,3,29863,3,29867,3,3,29873,
3,3,29879,29881,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
29917,3,29921,3,3,29927,3,3,3,3,3,3,3,3,3,29947,3,3,
3,3,3,29959,3,3,3,3,3,3,3,3,3,3,3,29983,3,3,29989,3,3,
3,3,3,3,3,3,3,3,30011,30013,3,3,3,3,3,3,3,30029,3,3,3,
3,3,3,3,3,30047,3,3,3,3,3,30059,3,3,3,3,3,30071,3,3,3,
3,3,3,3,3,30089,30091,3,3,30097,3,3,30103,3,3,30109,
3,30113,3,3,30119,3,3,3,3,3,3,30133,3,30137,30139,3,
3,3,3,3,3,3,3,3,3,30161,3,3,3,30169,3,3,3,3,3,30181,3,
3,30187,3,3,3,3,30197,3,3,30203,3,3,3,30211,3,3,3,3,3,
30223,3,3,3,3,3,3,3,3,30241,3,3,3,3,3,30253,3,3,
30259,3,3,3,3,30269,30271,3,3,3,3,3,3,3,3,3,3,30293,
3,3,3,3,3,3,30307,3,3,30313,3,3,30319,3,30323,3,3,3,
3,3,3,3,3,30341,3,3,30347,3,3,3,3,3,3,3,3,3,30367,3,3,
3,3,3,3,3,3,3,3,30389,30391,3,3,3,3,3,30403,3,3,3,3,3,
3,3,3,3,3,3,30427,3,30431,3,3,3,3,3,3,3,3,30449,3,3,3,
3,3,3,3,3,30467,30469,3,3,3,3,3,3,3,3,3,3,30491,
30493,3,30497,3,3,3,3,3,30509,3,3,3,30517,3,3,3,3,3,
30529,3,3,3,3,30539,3,3,3,3,3,3,30553,3,30557,30559,
3,3,3,3,3,3,3,3,30577,3,3,3,3,3,3,3,30593,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,30631,3,3,30637,3,3,30643,3,3,
30649,3,3,3,3,3,30661,3,3,3,3,30671,3,3,30677,3,3,3,
3,3,30689,3,3,3,30697,3,3,30703,3,30707,3,3,30713,3,
3,3,3,3,3,30727,3,3,3,3,3,3,3,3,3,3,3,3,3,3,30757,3,3,
30763,3,3,3,3,30773,3,3,3,30781,3,3,3,3,3,3,3,3,3,3,
30803,3,3,30809,3,3,3,30817,3,3,3,3,3,30829,3,3,3,3,
30839,30841,3,3,3,3,30851,30853,3,3,30859,3,3,3,3,
30869,30871,3,3,3,3,30881,3,3,3,3,3,30893,3,3,3,3,3,
3,3,3,30911,3,3,3,3,3,3,3,3,3,30931,3,3,30937,3,30941,
3,3,3,30949,3,3,3,3,3,3,3,3,3,3,30971,3,3,30977,3,3,
30983,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31013,3,3,31019,3,3,
3,3,3,3,31033,3,3,31039,3,3,3,3,3,31051,3,3,3,3,3,
31063,3,3,31069,3,3,3,3,31079,31081,3,3,3,3,31091,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,31121,31123,3,3,3,3,3,3,3,
31139,3,3,3,31147,3,31151,31153,3,3,31159,3,3,3,3,3,
3,3,3,31177,3,31181,31183,3,3,31189,3,31193,3,3,3,3,
3,3,3,3,3,3,3,3,31219,3,31223,3,3,3,31231,3,3,31237,
3,3,3,3,31247,31249,3,31253,3,3,31259,3,3,3,31267,3,
31271,3,3,31277,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31307,3,3,
3,3,3,31319,31321,3,3,31327,3,3,31333,3,31337,3,3,3,
3,3,3,3,3,3,31357,3,3,3,3,3,3,3,3,3,3,31379,3,3,3,
31387,3,31391,31393,3,31397,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31469,3,3,3,
31477,3,31481,3,3,3,31489,3,3,3,3,3,3,3,3,3,3,31511,
31513,3,31517,3,3,3,3,3,3,31531,3,3,3,3,31541,31543,
3,31547,3,3,3,3,3,3,3,3,3,31567,3,3,31573,3,3,3,3,
31583,3,3,3,3,3,3,3,3,31601,3,3,31607,3,3,3,3,3,3,3,3,
3,31627,3,3,3,3,3,3,3,31643,3,3,31649,3,3,3,31657,3,
3,31663,3,31667,3,3,3,3,3,3,3,3,3,31687,3,3,3,3,3,
31699,3,3,3,3,3,3,3,3,3,3,31721,31723,3,31727,31729,
3,3,3,3,3,31741,3,3,3,3,31751,3,3,3,3,3,3,3,3,31769,
31771,3,3,3,3,3,3,3,3,3,3,31793,3,3,31799,3,3,3,3,3,3,
3,3,31817,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31847,31849,3,3,
3,3,31859,3,3,3,3,3,3,31873,3,3,3,3,31883,3,3,3,
31891,3,3,3,3,3,3,3,31907,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,31957,3,3,31963,3,3,3,3,31973,3,3,3,
31981,3,3,3,3,31991,3,3,3,3,3,32003,3,3,32009,3,3,3,
3,3,3,3,3,32027,32029,3,3,3,3,3,3,3,3,3,3,32051,3,3,
32057,32059,3,32063,3,3,32069,3,3,3,32077,3,3,
32083,3,3,32089,3,3,3,3,32099,3,3,3,3,3,3,3,3,32117,
32119,3,3,3,3,3,3,3,3,3,3,32141,32143,3,3,3,3,3,3,3,
32159,3,3,3,3,3,3,32173,3,3,3,3,32183,3,3,32189,
32191,3,3,3,3,3,32203,3,3,3,3,32213,3,3,3,3,3,3,3,3,3,
32233,3,32237,3,3,3,3,3,3,32251,3,3,32257,3,32261,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,32297,32299,3,32303,3,
3,32309,3,3,3,3,3,32321,32323,3,32327,3,3,3,3,3,3,
32341,3,3,3,3,3,32353,3,3,32359,3,32363,3,3,32369,
32371,3,3,32377,3,32381,3,3,3,3,3,3,3,3,3,32401,3,3,
3,3,32411,32413,3,3,3,3,32423,3,3,32429,3,3,3,3,3,
32441,32443,3,3,3,3,3,3,3,3,3,3,3,32467,3,3,3,3,3,
32479,3,3,3,3,3,32491,3,3,32497,3,3,32503,3,32507,3,
3,3,3,3,3,3,3,3,3,3,32531,32533,3,32537,3,3,3,3,3,3,3,
3,3,3,3,32561,32563,3,3,32569,3,32573,3,3,32579,3,3,
3,32587,3,3,3,3,3,3,3,32603,3,3,32609,32611,3,3,3,3,
32621,3,3,3,3,3,32633,3,3,3,3,3,3,32647,3,3,32653,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,32687,3,3,32693,3,3,3,3,3,
3,32707,3,3,32713,3,32717,32719,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,32749,3,3,3,3,3,3,3,3,3,3,32771,3,3,3,32779,3,
32783,3,3,32789,3,3,3,32797,3,32801,32803,3,3,3,3,3,
3,3,3,3,3,3,3,3,32831,32833,3,3,32839,3,32843,3,3,3,
3,3,3,3,3,3,3,3,3,32869,3,3,3,3,3,3,3,3,32887,3,3,3,3,3,
3,3,3,3,3,32909,32911,3,3,32917,3,3,3,3,3,3,3,32933,3,
3,32939,32941,3,3,3,3,3,3,3,32957,3,3,3,3,3,32969,
32971,3,3,3,3,3,32983,3,32987,3,3,32993,3,3,32999,3,
3,3,3,3,3,33013,3,3,3,3,33023,3,3,33029,3,3,3,33037,
3,3,3,3,3,33049,3,33053,3,3,3,3,3,3,3,3,33071,33073,
3,3,3,3,33083,3,3,3,33091,3,3,3,3,3,3,3,33107,3,3,
33113,3,3,33119,3,3,3,3,3,3,3,3,3,3,3,3,3,3,33149,
33151,3,3,3,3,33161,3,3,3,3,3,3,3,3,33179,33181,3,3,
3,3,33191,3,3,3,33199,3,33203,3,3,3,33211,3,3,3,3,3,
33223,3,3,3,3,3,3,3,3,3,3,3,33247,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,33287,33289,3,3,3,3,3,33301,3,3,3,3,
33311,3,3,33317,3,3,3,3,3,33329,33331,3,3,3,3,3,
33343,3,33347,33349,3,33353,3,3,33359,3,3,3,3,3,3,3,
3,33377,3,3,3,3,3,3,33391,3,3,3,3,3,33403,3,3,33409,
3,33413,3,3,3,3,3,3,33427,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
33457,3,33461,3,3,3,33469,3,3,3,3,33479,3,3,3,33487,
3,3,33493,3,3,3,3,33503,3,3,3,3,3,3,3,3,33521,3,3,3,
33529,3,33533,3,3,3,3,3,3,33547,3,3,3,3,3,3,3,33563,
3,3,33569,3,3,3,33577,3,33581,3,3,33587,33589,3,3,3,
3,33599,33601,3,3,3,3,3,33613,3,33617,33619,3,
33623,3,3,33629,3,3,3,33637,3,33641,3,3,33647,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,33679,3,3,3,3,3,3,3,3,3,3,3,
33703,3,3,3,3,33713,3,3,3,33721,3,3,3,3,3,3,3,3,
33739,3,3,3,3,33749,33751,3,3,33757,3,3,3,3,33767,
33769,3,33773,3,3,3,3,3,3,3,3,33791,3,3,33797,3,3,3,
3,3,33809,33811,3,3,3,3,3,3,3,33827,33829,3,3,3,3,3,3,
3,3,3,3,33851,3,3,33857,3,3,33863,3,3,3,33871,3,3,3,
3,3,3,3,3,33889,3,33893,3,3,3,3,3,3,3,3,33911,3,3,3,3,
3,33923,3,3,3,33931,3,3,33937,3,33941,3,3,3,3,3,3,3,
3,3,33961,3,3,33967,3,3,3,3,3,3,3,3,3,3,3,3,3,3,33997,
3,3,3,3,3,3,3,3,3,3,34019,3,3,3,3,3,34031,34033,3,3,
34039,3,3,3,3,3,3,3,3,34057,3,34061,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,34123,3,34127,
34129,3,3,3,3,3,34141,3,3,34147,3,3,3,3,34157,34159,
3,3,3,3,3,34171,3,3,3,3,3,34183,3,3,3,3,3,3,3,3,3,3,3,3,
3,34211,34213,3,34217,3,3,3,3,3,3,34231,3,3,3,3,3,3,3,
3,3,3,34253,3,3,34259,34261,3,3,34267,3,3,34273,3,3,
3,3,34283,3,3,3,3,3,3,34297,3,34301,34303,3,3,3,3,
34313,3,3,34319,3,3,3,34327,3,3,3,3,34337,3,3,3,3,3,
3,34351,3,3,3,3,34361,3,3,34367,34369,3,3,3,3,3,
34381,3,3,3,3,3,3,3,3,3,3,34403,3,3,3,3,3,3,3,3,34421,
3,3,3,34429,3,3,3,3,34439,3,3,3,3,3,3,3,3,34457,3,3,3,
3,3,34469,34471,3,3,3,3,3,34483,3,34487,3,3,3,3,3,
34499,34501,3,3,3,3,34511,34513,3,3,34519,3,3,3,3,3,
3,3,3,34537,3,3,34543,3,3,34549,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,34583,3,3,34589,34591,3,3,3,3,3,34603,3,
34607,3,3,34613,3,3,3,3,3,3,3,3,34631,3,3,3,3,3,3,3,3,
34649,34651,3,3,3,3,3,3,3,34667,3,3,34673,3,3,34679,
3,3,3,34687,3,3,34693,3,3,3,3,34703,3,3,3,3,3,3,3,3,
34721,3,3,3,34729,3,3,3,3,34739,3,3,3,34747,3,3,3,3,
34757,34759,3,34763,3,3,3,3,3,3,3,3,34781,3,3,3,3,3,
3,3,3,3,3,3,3,34807,3,3,3,3,3,34819,3,3,3,3,3,3,3,3,3,3,
34841,34843,3,34847,34849,3,3,3,3,3,3,3,3,3,3,34871,
3,3,34877,3,3,34883,3,3,3,3,3,3,34897,3,3,3,3,3,3,3,
34913,3,3,34919,3,3,3,3,3,3,3,3,3,34939,3,3,3,3,
34949,3,3,3,3,3,34961,34963,3,3,3,3,3,3,3,3,34981,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,35023,3,35027,3,3,
3,3,3,3,3,3,3,3,3,35051,35053,3,3,35059,3,3,3,3,
35069,3,3,3,3,3,35081,35083,3,3,35089,3,3,3,3,35099,
3,3,3,35107,3,35111,3,3,35117,3,3,3,3,3,35129,3,3,3,3,
3,35141,3,3,3,35149,3,35153,3,3,35159,3,3,3,3,3,
35171,3,3,3,3,3,3,3,3,3,3,3,3,3,3,35201,3,3,3,3,3,3,3,3,
3,35221,3,3,35227,3,3,3,3,3,3,3,3,3,3,3,35251,3,3,
35257,3,3,3,3,35267,3,3,3,3,3,35279,35281,3,3,3,3,
35291,3,3,3,3,3,3,3,3,3,35311,3,3,35317,3,3,35323,3,
35327,3,3,3,3,3,35339,3,3,3,3,3,3,35353,3,3,3,3,
35363,3,3,3,3,3,3,3,3,35381,3,3,3,3,3,35393,3,3,3,
35401,3,3,35407,3,3,3,3,3,35419,3,35423,3,3,3,3,3,3,
35437,3,3,3,3,35447,35449,3,3,3,3,3,35461,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,35491,3,3,3,3,3,3,3,35507,35509,3,3,
3,3,3,35521,3,3,35527,3,35531,35533,3,35537,3,3,
35543,3,3,3,3,3,3,3,3,3,3,3,3,35569,3,35573,3,3,3,3,3,
3,3,3,35591,35593,3,35597,3,3,35603,3,3,3,3,3,3,
35617,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
35671,3,3,35677,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,35729,35731,3,3,3,3,3,3,3,35747,3,3,35753,
3,3,35759,3,3,3,3,3,35771,3,3,3,3,3,3,3,3,3,3,3,3,
35797,3,35801,35803,3,3,35809,3,3,3,3,3,3,3,3,3,3,
35831,3,3,35837,35839,3,3,3,3,3,35851,3,3,3,3,3,
35863,3,3,35869,3,3,3,3,35879,3,3,3,3,3,3,3,3,35897,
35899,3,3,3,3,3,35911,3,3,3,3,3,35923,3,3,3,3,35933,3,
3,3,3,3,3,3,3,35951,3,3,3,3,3,35963,3,3,35969,3,3,3,
35977,3,3,35983,3,3,3,3,35993,3,3,35999,3,3,3,36007,
3,36011,36013,3,36017,3,3,3,3,3,3,3,3,3,36037,3,3,3,3,
3,3,3,3,3,3,3,36061,3,3,36067,3,3,36073,3,3,3,3,
36083,3,3,3,3,3,3,36097,3,3,3,3,36107,36109,3,3,3,3,
3,3,3,3,3,3,36131,3,3,36137,3,3,3,3,3,3,36151,3,3,3,3,
36161,3,3,3,3,3,3,3,3,3,3,3,3,36187,3,36191,3,3,3,3,3,
3,3,3,36209,3,3,3,36217,3,3,3,3,3,36229,3,3,3,3,3,
36241,3,3,3,3,36251,3,3,3,3,3,36263,3,3,36269,3,3,3,
36277,3,3,3,3,3,3,3,36293,3,3,36299,3,3,3,36307,3,3,
36313,3,3,36319,3,3,3,3,3,3,3,3,3,3,36341,36343,3,3,
3,3,36353,3,3,3,3,3,3,3,3,3,36373,3,3,3,3,36383,3,3,
36389,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,36433,3,
3,3,3,3,3,3,3,36451,3,3,36457,3,3,3,3,36467,36469,3,
36473,3,3,36479,3,3,3,3,3,3,36493,3,36497,3,3,3,3,3,
3,3,3,3,3,3,3,36523,3,36527,36529,3,3,3,3,3,36541,3,
3,3,3,36551,3,3,3,36559,3,36563,3,3,3,36571,3,3,3,3,
3,36583,3,36587,3,3,3,3,3,36599,3,3,3,36607,3,3,3,3,
3,3,3,3,3,3,36629,3,3,3,36637,3,3,36643,3,3,3,3,
36653,3,3,3,3,3,3,3,3,36671,3,3,36677,3,3,36683,3,3,
3,36691,3,3,36697,3,3,3,3,3,36709,3,36713,3,3,3,
36721,3,3,3,3,3,3,3,3,36739,3,3,3,3,36749,3,3,3,3,3,
36761,3,3,36767,3,3,3,3,3,36779,36781,3,3,36787,3,
36791,36793,3,3,3,3,3,3,3,36809,3,3,3,3,3,36821,3,3,
3,3,3,36833,3,3,3,3,3,3,36847,3,3,3,3,36857,3,3,3,3,3,
3,36871,3,3,36877,3,3,3,3,36887,3,3,3,3,3,36899,
36901,3,3,3,3,3,36913,3,3,36919,3,36923,3,3,36929,
36931,3,3,3,3,3,36943,3,36947,3,3,3,3,3,3,3,3,3,3,3,3,
36973,3,3,36979,3,3,3,3,3,3,3,3,36997,3,3,37003,3,3,
3,3,37013,3,3,37019,37021,3,3,3,3,3,3,3,3,37039,3,3,
3,3,37049,3,3,3,37057,3,37061,3,3,3,3,3,3,3,3,3,3,3,3,
37087,3,3,3,3,37097,3,3,3,3,3,3,3,3,3,37117,3,3,37123,
3,3,3,3,3,3,3,37139,3,3,3,3,3,3,3,3,3,37159,3,3,3,3,3,
37171,3,3,3,3,37181,3,3,3,37189,3,3,3,3,37199,37201,
3,3,3,3,3,3,3,37217,3,3,37223,3,3,3,3,3,3,3,3,3,37243,
3,3,3,3,37253,3,3,3,3,3,3,3,3,3,37273,3,37277,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,37307,37309,3,37313,3,3,3,37321,
3,3,3,3,3,3,3,37337,37339,3,3,3,3,3,3,3,3,37357,3,
37361,37363,3,3,37369,3,3,3,3,37379,3,3,3,3,3,3,3,3,
37397,3,3,3,3,3,37409,3,3,3,3,3,3,37423,3,3,3,3,3,3,3,
3,37441,3,3,37447,3,3,3,3,3,3,3,37463,3,3,3,3,3,3,3,3,
3,37483,3,3,37489,3,37493,3,3,3,37501,3,3,37507,3,
37511,3,3,37517,3,3,3,3,3,37529,3,3,3,37537,3,3,3,3,
37547,37549,3,3,3,3,3,37561,3,3,37567,3,37571,
37573,3,3,37579,3,3,3,3,37589,37591,3,3,3,3,3,3,3,
37607,3,3,3,3,3,37619,3,3,3,3,3,3,37633,3,3,3,3,
37643,3,3,37649,3,3,3,37657,3,3,37663,3,3,3,3,3,3,3,
3,3,3,3,3,3,37691,37693,3,3,37699,3,3,3,3,3,3,3,3,
37717,3,3,3,3,3,3,3,3,3,3,3,3,3,3,37747,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,37781,37783,3,3,3,3,3,3,3,37799,3,3,3,
3,3,37811,37813,3,3,3,3,3,3,3,3,37831,3,3,3,3,3,3,3,
37847,3,3,37853,3,3,3,37861,3,3,3,3,37871,3,3,3,
37879,3,3,3,3,37889,3,3,3,37897,3,3,3,3,37907,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,37951,3,3,37957,3,3,
37963,3,37967,3,3,3,3,3,3,3,3,3,37987,3,37991,37993,
3,37997,3,3,3,3,3,3,38011,3,3,3,3,3,3,3,3,3,3,3,3,3,
38039,3,3,3,38047,3,3,38053,3,3,3,3,3,3,3,38069,3,3,
3,3,3,3,38083,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38113,3,3,
38119,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38149,3,38153,3,3,3,
3,3,3,38167,3,3,3,3,38177,3,3,38183,3,3,38189,3,3,3,
38197,3,38201,3,3,3,3,3,3,3,3,38219,3,3,3,3,3,38231,
3,3,38237,38239,3,3,3,3,3,3,3,3,3,3,38261,3,3,3,3,3,
38273,3,3,3,38281,3,3,38287,3,3,3,3,3,38299,3,38303,
3,3,3,3,3,3,38317,3,38321,3,3,38327,38329,3,38333,3,
3,3,3,3,3,3,3,38351,3,3,3,3,3,3,3,3,3,38371,3,3,38377,
3,3,3,3,3,3,3,38393,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
38431,3,3,3,3,3,3,3,38447,38449,3,38453,3,3,38459,
38461,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38501,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38543,3,3,3,3,3,3,
38557,3,38561,3,3,38567,38569,3,3,3,3,3,3,3,3,3,3,3,
38593,3,3,3,3,38603,3,3,38609,38611,3,3,3,3,3,3,3,3,
38629,3,3,3,3,38639,3,3,3,3,3,38651,38653,3,3,3,3,3,
3,3,38669,38671,3,3,38677,3,3,3,3,3,3,3,38693,3,3,
38699,3,3,3,38707,3,38711,38713,3,3,3,3,38723,3,3,
38729,3,3,3,38737,3,3,3,3,38747,38749,3,3,3,3,3,3,3,
3,38767,3,3,3,3,3,3,3,38783,3,3,3,38791,3,3,3,3,3,
38803,3,3,3,3,3,3,3,3,38821,3,3,3,3,3,38833,3,3,
38839,3,3,3,3,3,38851,3,3,3,3,38861,3,3,38867,3,3,
38873,3,3,3,3,3,3,3,3,38891,3,3,3,3,3,38903,3,3,3,3,3,
3,38917,3,38921,38923,3,3,3,3,38933,3,3,3,3,3,3,3,3,
3,38953,3,3,38959,3,3,3,3,3,38971,3,3,38977,3,3,3,3,
3,3,3,38993,3,3,3,3,3,3,3,3,3,3,3,3,39019,3,39023,3,3,
3,3,3,3,3,3,39041,39043,3,39047,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,39079,3,3,3,3,39089,3,3,3,39097,3,3,39103,3,
39107,3,3,39113,3,3,39119,3,3,3,3,3,3,39133,3,3,
39139,3,3,3,3,3,3,3,3,39157,3,39161,39163,3,3,3,3,3,
3,3,3,39181,3,3,3,3,39191,3,3,3,39199,3,3,3,3,39209,
3,3,3,39217,3,3,3,3,39227,39229,3,39233,3,3,39239,
39241,3,3,3,3,39251,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,39293,3,3,3,39301,3,3,3,3,3,39313,3,39317,3,3,
39323,3,3,3,3,3,3,3,3,39341,39343,3,3,3,3,3,3,3,
39359,3,3,3,39367,3,39371,39373,3,3,3,3,39383,3,3,3,
3,3,3,39397,3,3,3,3,3,39409,3,3,3,3,39419,3,3,3,3,3,3,
3,3,3,39439,3,39443,3,3,3,39451,3,3,3,3,39461,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,39499,3,39503,3,3,39509,
39511,3,3,3,3,39521,3,3,3,3,3,3,3,3,3,39541,3,3,3,3,
39551,3,3,3,3,3,39563,3,3,39569,3,3,3,3,3,39581,3,3,
3,3,3,3,3,3,3,3,3,3,39607,3,3,3,3,3,39619,3,39623,3,3,
3,39631,3,3,3,3,3,3,3,3,3,3,3,3,3,39659,3,3,3,39667,3,
39671,3,3,3,39679,3,3,3,3,3,3,3,3,3,3,3,39703,3,3,
39709,3,3,3,3,39719,3,3,3,39727,3,3,39733,3,3,3,3,3,
3,3,39749,3,3,3,3,3,39761,3,3,3,39769,3,3,3,3,39779,
3,3,3,3,3,39791,3,3,3,39799,3,3,3,3,3,3,3,3,3,3,39821,
3,3,39827,39829,3,3,3,3,39839,39841,3,3,39847,3,3,3,
3,39857,3,3,39863,3,3,39869,3,3,3,39877,3,3,39883,3,
39887,3,3,3,3,3,3,39901,3,3,3,3,3,3,3,3,3,3,3,3,3,
39929,3,3,3,39937,3,3,3,3,3,3,3,39953,3,3,3,3,3,3,3,3,
39971,3,3,3,39979,3,39983,3,3,39989,3,3,3,3,3,3,3,3,
3,40009,3,40013,3,3,3,3,3,3,3,3,40031,3,3,40037,
40039,3,3,3,3,3,3,3,3,3,3,3,40063,3,3,3,3,3,3,3,3,3,3,3,
40087,3,3,40093,3,3,40099,3,3,3,3,3,40111,3,3,3,3,3,
40123,3,40127,40129,3,3,3,3,3,3,3,3,3,3,40151,40153,
3,3,3,3,40163,3,3,40169,3,3,3,40177,3,3,3,3,3,40189,
3,40193,3,3,3,3,3,3,3,3,3,40213,3,3,3,3,3,3,3,3,40231,
3,3,40237,3,40241,3,3,3,3,3,40253,3,3,3,3,3,3,3,3,3,3,
3,40277,3,3,40283,3,3,40289,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,40343,3,3,3,40351,3,3,40357,
3,40361,3,3,3,3,3,3,3,3,3,3,3,3,40387,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,40423,3,40427,40429,3,40433,3,3,3,3,
3,3,3,3,3,3,3,3,40459,3,3,3,3,3,40471,3,3,3,3,3,40483,
3,40487,3,3,40493,3,3,40499,3,3,3,40507,3,3,3,3,3,
40519,3,3,3,3,40529,40531,3,3,3,3,3,40543,3,3,3,3,3,
3,3,40559,3,3,3,3,3,3,3,3,40577,3,3,40583,3,3,3,
40591,3,3,40597,3,3,3,3,3,40609,3,3,3,3,3,3,3,3,
40627,3,3,3,3,40637,40639,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,40693,3,40697,40699,3,3,3,3,
40709,3,3,3,3,3,3,3,3,3,3,3,3,3,3,40739,3,3,3,3,3,
40751,3,3,3,40759,3,40763,3,3,3,40771,3,3,3,3,3,3,3,
40787,3,3,3,3,3,3,40801,3,3,3,3,3,40813,3,3,40819,3,
40823,3,3,40829,3,3,3,3,3,40841,3,3,40847,40849,3,
40853,3,3,3,3,3,3,40867,3,3,3,3,3,40879,3,40883,3,3,
3,3,3,3,40897,3,3,40903,3,3,3,3,3,3,3,3,3,3,3,40927,3,
3,40933,3,3,40939,3,3,3,3,40949,3,3,3,3,3,40961,3,3,
3,3,3,40973,3,3,3,3,3,3,3,3,3,40993,3,3,3,3,3,3,3,3,
41011,3,3,41017,3,3,41023,3,3,3,3,3,3,3,41039,3,3,3,
41047,3,41051,3,3,41057,3,3,3,3,3,3,3,3,3,41077,3,
41081,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,41113,3,41117,3,3,3,
3,3,3,41131,3,3,3,3,41141,41143,3,3,41149,3,3,3,3,3,
41161,3,3,3,3,3,3,3,41177,41179,3,41183,3,3,41189,3,
3,3,3,3,41201,41203,3,3

München, 17. Februar 2023

Gottfried Färberböck

Language:

Language:

THE PRIME NUMBER SERIES

Infinite prime number formulas thanks to Eratosthenes