Eulers Primzahlenformel repariert

DIE PRIMZAHLENSERIE

Beitrag 27

Euler fand die bemerkenswerte Formel

$n^2+n+41,$

die für $n \in \mathbb{N}$ mit $n\ge 0$ eine ununterbrochene Folge von Primzahlen bis n=39 liefert.

Ab n=40 liefert die Formel scheinbar willkürlich abwechselnd zusammengesetzte Zahlen und Primzahlen.

Ich habe die Formel $n^2+n+41$ mit einem Ausdruck multipliziert, der zusammengesetzte Werte erkennt und auf 0 setzt und nur Primzahlen anzeigt.

Die reparierte Formel sieht so aus:

$(n^2+n+41)\prod\limits_{k=0} ^\frac{\sqrt{n^2+n+41}-3}{2} \lceil\sin^2(\frac{n^2+n+41}{2k+3}\pi)\rceil$

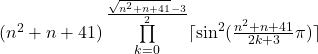
Diese Formel liefert alle Primzahlen der ursprünglichen Eulerformel. Ob es unendlich viele der Form $n^2+n+41$ gibt, konnte bisher nicht bewiesen werden.

Falls man alle Primzahlen größer 2 heraus filtern will, sieht die Formel so aus:

$(2n+3)\prod\limits_{k=0} ^\frac{\sqrt{2n+3}-3}{2} \lceil\sin^2(\frac{n-k}{2n+3}\pi)\rceil$

München, 3. Februar 2026

Gottfried Färberböck

Sprache:

Sprache:

DIE PRIMZAHLENSERIE

Eulers Primzahlenformel repariert