Unendlich viele Primzahlformeln dank Eratosthenes
DIE PRIMZAHLENSERIE
Beitrag 13
Unendlich viele Primzahlformeln dank Eratosthenes
Es gibt unendlich viele Primzahlformeln. Jede einzelne dieser Formeln liefert in vorbestimmten Bereichen ausschließlich Primzahlen und zudem alle Primzahlen neben der 3, die in dem jeweiligen Bereich überhaupt existieren.
Dies sind gewagte Behauptungen.
In Beitrag 9, DIE DUALE PRIMZAHLFUNKTION wurde bewiesen:
Die Primzahlfunktion p(n) liefert für n ∈ ℕ größer 0 immer eine Primzahl größer 2.
Die Primzahlfunktion p(n) hat für vorhersagbare
n ∈ ℕ größer 0 immer die Primzahl 3 und für die restlichen n ∈ ℕ größer 0 ALLE PRIMZAHLEN GRÖSSER 3 als Ergebnis.
Die duale Primzahlfunktion lautet:
p(n)=2n*t(n)+3
In Beitrag 7, DER n-PRIMZAHLTEST wurde bewiesen:
Für ein gewähltes n>0 aus der Menge der natürlichen Zahlen ist t(n) entweder 0 oder 1.
Ist t(n)=0, dann ist 2n+3 für das gewählte n nicht prim.
Ist t(n)=1, dann ist 2n+3 für das gewählte n prim.
![]()
mit
![]()
wobei n ∈ ℕ und n ≥ 1 sowie k ∈ ℕ und k ≥ 0.
In p(n) und in t(n) ist n die Variable und ![]() die abhängige Variable.
die abhängige Variable.
Was passiert, wenn ![]() ∈ ℕ eine frei wählbare Variable ist und n ∈ ℕ ≥ 1 eine nach oben begrenzte Variable ist?
∈ ℕ eine frei wählbare Variable ist und n ∈ ℕ ≥ 1 eine nach oben begrenzte Variable ist?
Setzt man ![]() als Variable in p(n), ergibt dies
als Variable in p(n), ergibt dies
p(![]() )=2n*t(
)=2n*t(![]() )+3
)+3
Dies kann auch so geschrieben werden:
p(![]() )=3+2n*t(
)=3+2n*t(![]() )
)
![]()
Die Grundlage für alle Primzahlen größer 2 ist die potentielle Primzahlfunktion
ppot (n)=2n+3 ∧ n ∈ ℕ
Diese Funktion liefert alle ungeraden Zahlen größer 1, die aus allen Primzahlen größer 2 und allen zusammengesetzten, ungeraden Zahlen bestehen.
Die unendliche Zahlenfolge für ppot(n) sieht so aus:
3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,
39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,
71,73,75,77,79,81,83….
Nun sieben wir mittels der Funktion p(![]() ) ähnlich dem Sieb des Eratosthenes bzw. noch ähnlicher dem ungeraden Sieb. Allerdings tritt an die Stelle der gestrichenen Zahl jeweils eine 3.
) ähnlich dem Sieb des Eratosthenes bzw. noch ähnlicher dem ungeraden Sieb. Allerdings tritt an die Stelle der gestrichenen Zahl jeweils eine 3.
Ist ![]() =0, ergibt dies für n ∈ ℕ und
=0, ergibt dies für n ∈ ℕ und ![]() =1 die unendliche Zahlenfolge
=1 die unendliche Zahlenfolge
5,7,3,11,13,3,17,19,3,23,25,3,29,31,3,35,37,3,41,
43,3,47,49,3,53,55,3,59,61,3,65,67,3,71,73,3,77,79,
3,83….
In dieser Zahlenfolge sind alle durch 3 teilbaren Zahlen ausgesiebt, indem sie jeweils in die Zahl 3 aus 2n*0+3 umgewandelt wurden.
Weiter können wir sehen, daß alle Zahlen kleiner 25=5² prim sind.
Dies ergibt die 1.Primzahlformel
![]()
gültig für ![]()
Und dann ist da noch eines: Die kleinste Primzahl außer 3 ist 5.
Die nächste Siebung ergibt mit ![]() =1 und
=1 und ![]() =2 die unendliche Zahlenfolge
=2 die unendliche Zahlenfolge
7,3,11,13,3,17,19,3,23,3,3,29,31,3,3,37,3,41,43,3,
47,49,3,53,3,3,59,61,3,3,67,3,71,73,3,77,79,3,83,….
In dieser unendlichen Zahlenfolge sind alle durch 3 und 5 teilbaren Zahlen ausgesiebt.
Weiter können wir sehen, daß alle Zahlen kleiner 49=7² prim sind.
Dies ergibt die 2.Primzahlformel
![]()
gültig für ![]()
Und die kleinste Primzahl außer 3 ist 7.
Hoppla! Gibt es da etwa Gesetzmäßigkeiten?
Prüfen wir mal weiter, indem wir willkürlich ![]() =5 setzen.
=5 setzen.
Die resultierende unendliche Zahlenfolge dürfte demnach keine zusammengesetzte Zahl beinhalten, die durch 3 teilbar ist und keine Zahlen, die durch 5,7,9,11 und 13 teilbar sind. Außerdem müßten alle Zahlen kleiner 15²=225 prim sein. Und zudem müßte die kleinste Primzahl außer 3 die 17 sein, da
![]()
![]() =5+1=6
=5+1=6
Ist das wirklich so?
Wir setzen ![]() =5 in p(
=5 in p(![]() ) und erhalten die 6.Formel
) und erhalten die 6.Formel
![]()
![]()
und erhalten für n ab
![]()
die unendliche Zahlenfolge
3,17,19,3,23,3,3,29,31,3,3,37,3,41,43,3,47,
3,3,53,3,3,59,61,3,3,67,3,71,73,3,3,79,3,83,3,3,89,3,
3,3,97,3,101,103,3,107,109,3,113,3,3,3,3,3,3,127,3,
131,3,3,137,139,3,3,3,3,149,151,3,3,157,3,3,163,3,
167,3,3,173,3,3,179,181,3,3,3,3,191,193,3,197,199,
3,3,3,3,3,211,3,3,3,3,3,223,3,227,229,3,233,3,3,239,
241,3,3,3,3,251,3,3,257,3,3,263,3,3,269,271,3,3,277,
3,281,283,3,3,289,3,293,3,3,3,3,3,3,307,3,311,313,3,
317,3,3,323,3,3,3,331,3,3,337,3,3,3,3,347,349,3,353,
3,3,359,361,3,3,367,3,3,373,3,3,379,3,383,3,3,389,
391,3,3,397,3,401,3,….
Und tatsächlich:
Die kleinste Primzahl außer 3 ist 17.
Alle Zahlen kleiner 15²=225 sind prim.
Damit ist die 6.Formel die 6.Primzahlformel.
Tatsächlich ist es sogar so, daß alle Zahlen kleiner 17²=289 prim sind. Grund hierfür ist, daß 15 teilbar ist und 17 die nächste Primzahl nach 13 ist.
Hinsichtlich der resultierenden Zahlenfolge dürften demnach keine durch 3,5,7,9,11 und 13 teilbaren Zahlen mehr vorhanden sein außer den 3er-Ziffern, die zusammengesetzte Zahlen ersetzen. Und tatsächlich: Es sind alle zusammengesetzten Zahlen, die durch 3 teilbar sind und alle Zahlen, die durch 5,7,9,11 und 13 teilbar sind ausgesiebt, d.h. durch 3 ersetzt.
Für den weiteren Beweis setzen wir
![]()
und bezeichnen s(k,n) als Siebfaktorfunktion.
Behauptung : Die Siebfaktorfunktion s(k,n) kann nur die Werte 0 oder 1 annehmen.
Hat die Siebfaktorfunktion s(k,n) den Wert 0, dann sind sowohl 2n+3 als auch n-k durch 2k+3 teilbar.
Hat die Siebfaktorfunktion s(k,n) den Wert 1, dann sind weder 2n+3 noch n-k durch 2k+3 teilbar.
Beweis:
In Beitrag 6 DIE BESTIMMUNG ALLER PRIMZAHLEN IN EINEM GEWÄHLTEN BEREICH MIT DER n-METHODE wurde bewiesen, daß im Falle von
n=nkm = 2k²+6k+3+m(2k+3) ʌ k, m ∈ ℕ
n in
2n+3 ʌ n ∈ ℕ
alle ungeraden zusammengesetzten Zahlen liefert und im Falle von
n≠nkm
n in 2n+3 alle Primzahlen größer 2 liefert.
Fall 1: s(k,n)=0
Beweis 1: In diesem Fall muß n=nkm sein.
n=nkm =2k²+6k+3+m(2k+3) eingesetzt in
![]()
![]()
![]()
![]()
![]()
Was zu beweisen war.
Beweis 2: Ist n-k durch 2k+3 teilbar, dann ist das Produkt
![]()
Dies ergibt in s(k,n)
![]()
![]()
![]()
![]()
Was zu beweisen war.
Fall 2: s(k,n)=1
Dies bedeutet n-k ist nicht durch 2k+3 teilbar.
Beweis:
Ist n-k nicht durch 2k+3 teilbar, ist das Produkt mit n>k
![]()
Ist n tatsächlich immer größer als k?
Da
![]()
ist
![]()
Und das heißt weiter:
Jedes
![]()
Also ist es richtig, daß n immer größer als k ist. Somit gilt
![]()
Addieren wir bei jedem Term k hinzu, ergibt dies:
![]()
Dividieren wir jeden Term durch n≥1, ergibt dies:
![]()
Da k<n gilt
![]()
und
![]()
ist
![]()
Was zu beweisen war.
Somit ist dieser Term imstande, jede ungerade zusammengesetzte Zahl in Abhängigkeit von k, auszusieben.
Damit ist bewiesen, daß jede unendliche Zahlenfolge für alle n≥1 in
![]()
keine zusammengesetzte, ungerade Zahl, die durch 2k+3 von k=0 bis k=![]() teilbar ist, enthalten kann.
teilbar ist, enthalten kann.
Nun gilt es zu untersuchen, ob in jeder Zahlenfolge ![]() mit
mit ![]() ≤ n ≤
≤ n ≤ ![]()
wobei
![]()
und
![]()
neben der 3 auschließlich und alle Primzahlen enthalten sind, die in diesem Bereich existieren. Für die 1., 2. und 6. Primzahlformel trifft dies auf alle Fälle zu. Doch es gibt noch unendlich viele andere Fälle.
Zunächst zu ![]() . Daraus folgt die 1.Primzahlformel, bei der schon der Nachweis erbracht wurde.
. Daraus folgt die 1.Primzahlformel, bei der schon der Nachweis erbracht wurde.
Nehmen wir an, die Behauptungen sind wahr, daß
![]()
im Bereich
![]()
und
![]()
für ![]() ausschließlich Primzahlen und neben der 3 alle Primzahlen liefert, die in diesem Bereich überhaupt existieren.
ausschließlich Primzahlen und neben der 3 alle Primzahlen liefert, die in diesem Bereich überhaupt existieren.
Wenn dies auch für ![]() zutrifft, wäre der Beweis komplett erbracht.
zutrifft, wäre der Beweis komplett erbracht.
Dazu setzen wir
![]()
in
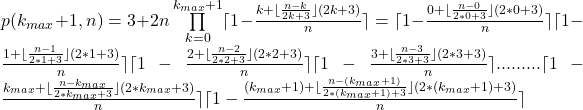
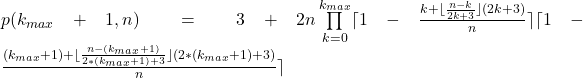
Nun wird überprüft, ob es eine ungerade Zahl bis
![]()
geben kann, die durch ![]() teilbar ist.
teilbar ist.
Dazu formen wir um
![]()
Da
![]()
und
![]() für
für ![]() ∈ ℕ
∈ ℕ
niemals teilbar ist, ist auch
![]()
niemals durch
![]()
teilbar.
Was zu beweisen war.
Somit gilt:
Die Funktion
![]()
liefert unendlich viele Formeln in Abhängigkeit von ![]() ∈ ℕ und k ≥ 0. Jede einzelne Formel liefert neben der Primzahl 3 alle Primzahlen im Bereich von n ∈ ℕ und n ≥ 1 mit
∈ ℕ und k ≥ 0. Jede einzelne Formel liefert neben der Primzahl 3 alle Primzahlen im Bereich von n ∈ ℕ und n ≥ 1 mit
![]()
![]()
ANMERKUNGEN: Die Funktion ![]() kann optimiert werden, indem die zusammengesetzten Siebfaktoren einfach weggelassen werden, sodaß nur noch die Prim-Siebfaktoren übrigbleiben. Es muß aber sichergestellt sein, daß kein Prim-Siebfaktor gestrichen wird, da sonst die Ergebnisse nicht hundertprozentig sind. Die Streichung der unnötigen Siebfaktoren kann, sofern die Primzahlen im erforderlichen Bereich nicht bekannt sind, beispielsweise mit Hilfe des ungeraden Siebes erfolgen, indem man alle p² (beginnend bei 3²=9) und alle p.ten auf p² folgenden Siebfaktoren streicht bzw. einfach wegläßt. Der jeweils p.te Wert wird auch durch die Addition von 2p ab p² erreicht.
kann optimiert werden, indem die zusammengesetzten Siebfaktoren einfach weggelassen werden, sodaß nur noch die Prim-Siebfaktoren übrigbleiben. Es muß aber sichergestellt sein, daß kein Prim-Siebfaktor gestrichen wird, da sonst die Ergebnisse nicht hundertprozentig sind. Die Streichung der unnötigen Siebfaktoren kann, sofern die Primzahlen im erforderlichen Bereich nicht bekannt sind, beispielsweise mit Hilfe des ungeraden Siebes erfolgen, indem man alle p² (beginnend bei 3²=9) und alle p.ten auf p² folgenden Siebfaktoren streicht bzw. einfach wegläßt. Der jeweils p.te Wert wird auch durch die Addition von 2p ab p² erreicht.
Je größer ![]() gewählt wird, desto mehr und größere Primzahlen werden geliefert. Dies geht so weit, daß selbst der stärkste Computer, den es jemals geben wird, nicht mehr in der Lage sein wird, diese zu berechnen.
gewählt wird, desto mehr und größere Primzahlen werden geliefert. Dies geht so weit, daß selbst der stärkste Computer, den es jemals geben wird, nicht mehr in der Lage sein wird, diese zu berechnen.
AUFGABEN
Aufgabe 1: Wie lautet die Obergrenze für alle Primzahlformeln, die von der Funktion ![]() abgeleitet werden können? Wie lautet diese für die zehnte Primzahlformel?
abgeleitet werden können? Wie lautet diese für die zehnte Primzahlformel?
![]()
![]()
![]()
Aufgabe 2: Wie lautet die Untergrenze für alle Primzahlformeln, die von der Funktion ![]() abgeleitet werden können? Wie lautet diese für die zehnte Primzahlformel?
abgeleitet werden können? Wie lautet diese für die zehnte Primzahlformel?
![]()
Für die zehnte Primzahlformel lautet diese:
![]()
Aufgabe 3: Wie lautet die kleinste potentielle Primzahl größer 3 einer Primzahlformel, die alle Primzahlen in diesem Bereich liefert? Wie lauten diese konkret bei der zehnten Primzahlformel?
Die Untergrenze für die kleinste Primzahl größer 3 kann abgeleitet werden von
![]()
![]()
![]()
![]()
Im Falle der zehnten Primzahlformel ist ![]() . Dies ergibt
. Dies ergibt
![]()
![]()
Aufgabe 4: Wie lautet die größte potentielle Primzahl einer Primzahlformel, die alle Primzahlen in diesem Bereich liefert? Wie lautet diese konkret bei der zehnten Primzahlformel?
Die Obergrenze für die größte potentielle Primzahl kann abgeleitet werden von
![]()
![]()
![]()
Im Falle der zehnten Primzahlformel ist ![]() . Dies ergibt
. Dies ergibt
![]()
Aufgabe 5: In welchem Bereich liefert jede Primzahlformel, abgeleitet von der Funktion ![]() alle Zahlen, die prim sind? Wie lautet dieser Bereich konkret für die zehnte Primzahlformel?
alle Zahlen, die prim sind? Wie lautet dieser Bereich konkret für die zehnte Primzahlformel?
Antwort:
2![]() +4 < p < 4
+4 < p < 4![]() ² +20
² +20![]() +24
+24
Die zehnte Primzahlformel liefert im Bereich
22<p<528
ausschließlich Primzahlen und zudem sind dies alle Primzahlen, die es in diesem Bereich gibt.
Aufgabe 6: Wie lautet die Funktion, von der unendlich viele Primzahlformeln abgeleitet werden können? In welchem Bereich gelten die abgeleiteten Primzahlformeln?
![]()
![]()
![]()
![]()
Aufgabe 7: Bestimme die zehnte Primzahlformel.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aufgabe 8: Bestimme die Primzahlenfolge der zehnten Primzahlformel.
23,3,3,29,31,3,3,37,3,41,43,3,47,3,3,53,3,3,59,61,3,3,
67,3,71,73,3,3,79,3,83,3,3,89,3,3,3,97,3,101,103,3,107,
109,3,113,3,3,3,3,3,3,127,3,131,3,3,137,139,3,3,3,3,
149,151,3,3,157,3,3,163,3,167,3,3,173,3,3,179,181,3,
3,3,3,191,193,3,197,199,3,3,3,3,3,211,3,3,3,3,3,223,3,
227,229,3,233,3,3,239,241,3,3,3,3,251,3,3,257,3,3,
263,3,3,269,271,3,3,277,3,281,283,3,3,3,3,293,3,3,3,3,
3,3,307,3,311,313,3,317,3,3,3,3,3,3,331,3,3,337,3,3,3,
3,347,349,3,353,3,3,359,3,3,3,367,3,3,373,3,3,379,3,
383,3,3,389,3,3,3,397,3,401,3,3,3,409,3,3,3,3,419,421,
3,3,3,3,431,433,3,3,439,3,443,3,3,449,3,3,3,457,3,461,
463,3,467,3,3,3,3,3,479,3,3,3,487,3,491,3,3,3,499,3,
503,3,3,509,3,3,3,3,3,521,523,3,3
Aufgabe 9: Bestimme die optimierte zehnte Primzahlformel. Mit optimierter Primzahlformel ist gemeint, daß aus der Primzahlformel diejenigen Siebfaktoren entfernt wurden, bei denen 2k+3 eine zusammengesetzte Zahl ist. D.h. es werden tatsächlich nur die Siebfaktoren benötigt, bei denen 2k+3 prim ist.
![]()
![]()
![]()
Aufgabe 10: Bestimme die Primzahlenfolge der zehnten Primzahlformel ohne der Primzahl 3.
23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,
101,103,107,109,113,127,131,137,139,149,151,157,
163,167,173,179,181,191,193,197,199,211,223,227,
229,233,239,241,251,257,263,269,271,277,281,283,
293,307,311,313,317,331,337,347,349,353,359,367,
373,379,383,389,397,401,409,419,421,431,433,439,
443,449,457,461,463,467,479,487,491,499,503,509,
521,523
Aufgabe 11: Bestimme die hundertste Primzahlformel und die dazugehörige Primzahlenfolge.
![]()
![]()
![]()
![]()
![]() …….
…….
![]()
100 ≤ n ≤ 20602
Die Primzahlenfolge für die hundertste Primzahlformel ist
3,3,3,3,211,3,3,3,3,3,223,3,227,229,3,233,3,3,239,
241,3,3,3,3,251,3,3,257,3,3,263,3,3,269,271,3,3,277,
3,281,283,3,3,3,3,293,3,3,3,3,3,3,307,3,311,313,3,
317,3,3,3,3,3,3,331,3,3,337,3,3,3,3,347,349,3,353,3,
3,359,3,3,3,367,3,3,373,3,3,379,3,383,3,3,389,3,3,3,
397,3,401,3,3,3,409,3,3,3,3,419,421,3,3,3,3,431,433,
3,3,439,3,443,3,3,449,3,3,3,457,3,461,463,3,467,3,3,
3,3,3,479,3,3,3,487,3,491,3,3,3,499,3,503,3,3,509,3,
3,3,3,3,521,523,3,3,3,3,3,3,3,3,541,3,3,547,3,3,3,3,
557,3,3,563,3,3,569,571,3,3,577,3,3,3,3,587,3,3,593,
3,3,599,601,3,3,607,3,3,613,3,617,619,3,3,3,3,3,631,
3,3,3,3,641,643,3,647,3,3,653,3,3,659,661,3,3,3,3,3,
673,3,677,3,3,683,3,3,3,691,3,3,3,3,701,3,3,3,709,3,
3,3,3,719,3,3,3,727,3,3,733,3,3,739,3,743,3,3,3,751,
3,3,757,3,761,3,3,3,769,3,773,3,3,3,3,3,3,787,3,3,3,3,
797,3,3,3,3,3,809,811,3,3,3,3,821,823,3,827,829,3,3,
3,3,839,3,3,3,3,3,3,853,3,857,859,3,863,3,3,3,3,3,3,
877,3,881,883,3,887,3,3,3,3,3,3,3,3,3,907,3,911,3,3,3,
919,3,3,3,3,929,3,3,3,937,3,941,3,3,947,3,3,953,3,3,
3,3,3,3,967,3,971,3,3,977,3,3,983,3,3,3,991,3,3,997,
3,3,3,3,3,1009,3,1013,3,3,1019,1021,3,3,3,3,1031,
1033,3,3,1039,3,3,3,3,1049,1051,3,3,3,3,1061,1063,3,
3,1069,3,3,3,3,3,3,3,3,1087,3,1091,1093,3,1097,3,3,
1103,3,3,1109,3,3,3,1117,3,3,1123,3,3,1129,3,3,3,3,3,
3,3,3,3,3,1151,1153,3,3,3,3,1163,3,3,3,1171,3,3,3,3,
1181,3,3,1187,3,3,1193,3,3,3,1201,3,3,3,3,3,1213,3,
1217,3,3,1223,3,3,1229,1231,3,3,1237,3,3,3,3,3,1249,
3,3,3,3,1259,3,3,3,3,3,3,3,3,1277,1279,3,1283,3,3,
1289,1291,3,3,1297,3,1301,1303,3,1307,3,3,3,3,3,
1319,1321,3,3,1327,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
1361,3,3,1367,3,3,1373,3,3,3,1381,3,3,3,3,3,3,3,3,
1399,3,3,3,3,1409,3,3,3,3,3,3,1423,3,1427,1429,3,
1433,3,3,1439,3,3,3,1447,3,1451,1453,3,3,1459,3,3,3,
3,3,1471,3,3,3,3,1481,1483,3,1487,1489,3,1493,3,3,
1499,3,3,3,3,3,1511,3,3,3,3,3,1523,3,3,3,1531,3,3,3,3,
3,1543,3,3,1549,3,1553,3,3,1559,3,3,3,1567,3,1571,3,
3,3,1579,3,1583,3,3,3,3,3,3,1597,3,1601,3,3,1607,
1609,3,1613,3,3,1619,1621,3,3,1627,3,3,3,3,1637,3,3,
3,3,3,3,3,3,3,1657,3,3,1663,3,1667,1669,3,3,3,3,3,3,
3,3,3,3,3,1693,3,1697,1699,3,3,3,3,1709,3,3,3,3,3,
1721,1723,3,3,3,3,1733,3,3,3,1741,3,3,1747,3,3,1753,
3,3,1759,3,3,3,3,3,3,3,3,1777,3,3,1783,3,1787,1789,
3,3,3,3,3,1801,3,3,3,3,1811,3,3,3,3,3,1823,3,3,3,1831,
3,3,3,3,3,3,3,1847,3,3,3,3,3,3,1861,3,3,1867,3,1871,
1873,3,1877,1879,3,3,3,3,1889,3,3,3,3,3,1901,3,3,
1907,3,3,1913,3,3,3,3,3,3,3,3,1931,1933,3,3,3,3,3,3,
3,1949,1951,3,3,3,3,3,3,3,3,3,3,1973,3,3,1979,3,3,3,
1987,3,3,1993,3,1997,1999,3,2003,3,3,3,2011,3,3,
2017,3,3,3,3,2027,2029,3,3,3,3,2039,3,3,3,3,3,3,
2053,3,3,3,3,2063,3,3,2069,3,3,3,3,3,2081,2083,3,
2087,2089,3,3,3,3,2099,3,3,3,3,3,2111,2113,3,3,3,3,3,
3,3,2129,2131,3,3,2137,3,2141,2143,3,3,3,3,2153,3,3,
3,2161,3,3,3,3,3,3,3,3,2179,3,3,3,3,3,3,3,3,3,3,3,
2203,3,2207,3,3,2213,3,3,3,2221,3,3,3,3,3,3,3,2237,
2239,3,2243,3,3,3,2251,3,3,3,3,3,3,3,2267,2269,3,
2273,3,3,3,2281,3,3,2287,3,3,2293,3,2297,3,3,3,3,3,
2309,2311,3,3,3,3,3,3,3,3,3,3,2333,3,3,2339,2341,3,3,
2347,3,2351,3,3,2357,3,3,3,3,3,3,2371,3,3,2377,3,
2381,2383,3,3,2389,3,2393,3,3,2399,3,3,3,3,3,2411,3,
3,2417,3,3,2423,3,3,3,3,3,3,2437,3,2441,3,3,2447,3,
3,3,3,3,2459,3,3,3,2467,3,3,2473,3,2477,3,3,3,3,3,3,
3,3,3,3,3,3,2503,3,3,3,3,3,3,3,3,2521,3,3,3,3,2531,3,
3,3,2539,3,2543,3,3,2549,2551,3,3,2557,3,3,3,3,3,3,
3,3,3,3,2579,3,3,3,3,3,2591,2593,3,3,3,3,3,3,3,2609,
3,3,3,2617,3,2621,3,3,3,3,3,2633,3,3,3,3,3,3,2647,3,
3,3,3,2657,2659,3,2663,3,3,3,2671,3,3,2677,3,3,
2683,3,2687,2689,3,2693,3,3,2699,3,3,3,2707,3,2711,
2713,3,3,2719,3,3,3,3,2729,2731,3,3,3,3,2741,3,3,3,
2749,3,2753,3,3,3,3,3,3,2767,3,3,3,3,2777,3,3,3,3,3,
2789,2791,3,3,2797,3,2801,2803,3,3,3,3,3,3,3,2819,3,
3,3,3,3,3,2833,3,2837,3,3,2843,3,3,3,2851,3,3,2857,
3,2861,3,3,3,3,3,3,3,3,2879,3,3,3,2887,3,3,3,3,2897,
3,3,2903,3,3,2909,3,3,3,2917,3,3,3,3,2927,3,3,3,3,3,
2939,3,3,3,3,3,3,2953,3,2957,3,3,2963,3,3,2969,2971,
3,3,3,3,3,3,3,3,3,3,3,3,3,2999,3001,3,3,3,3,3011,3,3,3,
3019,3,3023,3,3,3,3,3,3,3037,3,3041,3,3,3,3049,3,3,
3,3,3,3061,3,3,3067,3,3,3,3,3,3079,3,3083,3,3,3089,
3,3,3,3,3,3,3,3,3,3109,3,3,3,3,3119,3121,3,3,3,3,3,3,3,
3137,3,3,3,3,3,3,3,3,3,3,3,3,3163,3,3167,3169,3,3,3,
3,3,3181,3,3,3187,3,3191,3,3,3,3,3,3203,3,3,3209,3,
3,3,3217,3,3221,3,3,3,3229,3,3,3,3,3,3,3,3,3,3,3251,
3253,3,3257,3259,3,3,3,3,3,3271,3,3,3,3,3,3,3,3,3,3,
3,3,3,3299,3301,3,3,3307,3,3,3313,3,3,3319,3,3323,3,
3,3329,3331,3,3,3,3,3,3343,3,3347,3,3,3,3,3,3359,
3361,3,3,3,3,3371,3373,3,3,3,3,3,3,3,3389,3391,3,3,
3,3,3,3,3,3407,3,3,3413,3,3,3,3,3,3,3,3,3,3433,3,3,3,
3,3,3,3,3449,3,3,3,3457,3,3461,3463,3,3467,3469,3,3,
3,3,3,3,3,3,3,3,3491,3,3,3,3499,3,3,3,3,3,3511,3,3,
3517,3,3,3,3,3527,3529,3,3533,3,3,3539,3541,3,3,
3547,3,3,3,3,3557,3559,3,3,3,3,3,3571,3,3,3,3,3581,
3583,3,3,3,3,3593,3,3,3,3,3,3,3607,3,3,3613,3,3617,
3,3,3623,3,3,3,3631,3,3,3637,3,3,3643,3,3,3,3,3,3,3,
3659,3,3,3,3,3,3671,3673,3,3677,3,3,3,3,3,3,3691,3,
3,3697,3,3701,3,3,3,3709,3,3,3,3,3719,3,3,3,3727,3,
3,3733,3,3,3739,3,3,3,3,3,3,3,3,3,3,3761,3,3,3767,
3769,3,3,3,3,3779,3,3,3,3,3,3,3793,3,3797,3,3,3803,
3,3,3,3,3,3,3,3,3821,3823,3,3,3,3,3833,3,3,3,3,3,3,
3847,3,3851,3853,3,3,3,3,3863,3,3,3,3,3,3,3877,3,
3881,3,3,3,3889,3,3,3,3,3,3,3,3,3907,3,3911,3,3,3917,
3919,3,3923,3,3,3929,3931,3,3,3,3,3,3943,3,3947,3,3,
3,3,3,3,3,3,3,3967,3,3,3,3,3,3,3,3,3,3,3989,3,3,3,3,3,
4001,4003,3,4007,3,3,4013,3,3,4019,4021,3,3,4027,3,
3,3,3,3,3,3,3,3,3,4049,4051,3,3,4057,3,3,3,3,3,3,3,
4073,3,3,4079,3,3,3,3,3,4091,4093,3,3,4099,3,3,3,3,
3,4111,3,3,3,3,3,3,3,4127,4129,3,4133,3,3,4139,3,3,3,
3,3,3,4153,3,4157,4159,3,3,3,3,3,3,3,3,4177,3,3,3,3,
3,3,3,3,3,3,3,4201,3,3,3,3,4211,3,3,4217,4219,3,3,3,3,
4229,4231,3,3,3,3,4241,4243,3,3,3,3,4253,3,3,4259,
4261,3,3,3,3,4271,4273,3,3,3,3,4283,3,3,4289,3,3,3,
4297,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4327,3,3,3,3,4337,
4339,3,3,3,3,4349,3,3,3,4357,3,3,4363,3,3,3,3,4373,
3,3,3,3,3,3,3,3,4391,3,3,4397,3,3,3,3,3,4409,3,3,3,3,
3,4421,4423,3,3,3,3,3,3,3,3,4441,3,3,4447,3,4451,3,
3,4457,3,3,4463,3,3,3,3,3,3,3,3,4481,4483,3,3,3,3,
4493,3,3,3,3,3,3,4507,3,3,4513,3,4517,4519,3,4523,3,
3,3,3,3,3,3,3,3,3,3,4547,4549,3,3,3,3,3,4561,3,3,
4567,3,3,3,3,3,3,3,4583,3,3,3,4591,3,3,4597,3,3,
4603,3,3,3,3,3,3,3,3,4621,3,3,3,3,3,3,3,4637,4639,3,
4643,3,3,4649,4651,3,3,4657,3,3,4663,3,3,3,3,4673,3,
3,4679,3,3,3,3,3,4691,3,3,3,3,3,4703,3,3,3,3,3,3,3,3,
4721,4723,3,3,4729,3,4733,3,3,3,3,3,3,3,3,4751,3,3,
3,4759,3,3,3,3,3,3,3,3,3,3,3,4783,3,4787,4789,3,
4793,3,3,4799,4801,3,3,3,3,3,4813,3,4817,3,3,3,3,3,
3,4831,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4861,3,3,3,3,4871,
3,3,4877,3,3,3,3,3,4889,3,3,3,3,3,3,4903,3,3,4909,3,
3,3,3,4919,3,3,3,3,3,4931,4933,3,4937,3,3,4943,3,3,
3,4951,3,3,4957,3,3,3,3,4967,4969,3,4973,3,3,3,3,3,
3,4987,3,3,4993,3,3,4999,3,5003,3,3,5009,5011,3,3,3,
3,5021,5023,3,3,3,3,3,3,3,5039,3,3,3,3,3,5051,3,3,3,
5059,3,3,3,3,3,3,3,3,5077,3,5081,3,3,5087,3,3,3,3,3,
5099,5101,3,3,5107,3,3,5113,3,3,5119,3,3,3,3,3,3,3,3,
3,3,3,3,3,5147,3,3,5153,3,3,3,3,3,3,5167,3,5171,3,3,
3,5179,3,3,3,3,5189,3,3,3,5197,3,3,3,3,3,5209,3,3,3,
3,3,3,3,3,5227,3,5231,5233,3,5237,3,3,3,3,3,3,3,3,3,
3,3,5261,3,3,3,3,3,5273,3,3,5279,5281,3,3,3,3,3,3,3,
5297,3,3,5303,3,3,5309,3,3,3,3,3,3,5323,3,3,3,3,
5333,3,3,3,3,3,3,5347,3,5351,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,5381,3,3,5387,3,3,5393,3,3,5399,3,3,3,5407,3,3,
5413,3,5417,5419,3,3,3,3,3,5431,3,3,5437,3,5441,
5443,3,3,5449,3,3,3,3,3,3,3,3,3,3,5471,3,3,5477,
5479,3,5483,3,3,3,3,3,3,3,3,5501,5503,3,5507,3,3,3,
3,3,5519,5521,3,3,5527,3,5531,3,3,3,3,3,3,3,3,3,3,3,
3,5557,3,3,5563,3,3,5569,3,5573,3,3,3,5581,3,3,3,3,
5591,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,5623,3,3,3,3,3,3,3,
5639,5641,3,3,5647,3,5651,5653,3,5657,5659,3,3,3,3,
5669,3,3,3,3,3,3,5683,3,3,5689,3,5693,3,3,3,5701,3,
3,3,3,5711,3,3,5717,3,3,3,3,3,3,3,3,3,5737,3,5741,
5743,3,3,5749,3,3,3,3,3,3,3,3,3,3,3,3,3,3,5779,3,
5783,3,3,3,5791,3,3,3,3,5801,3,3,5807,3,3,5813,3,3,
3,5821,3,3,5827,3,3,3,3,3,5839,3,5843,3,3,5849,5851,
3,3,5857,3,5861,3,3,5867,5869,3,3,3,3,5879,5881,3,3,
3,3,3,3,3,5897,3,3,5903,3,3,3,3,3,3,3,3,3,5923,3,
5927,3,3,3,3,3,5939,3,3,3,3,3,3,5953,3,3,3,3,3,3,3,3,
3,3,3,3,3,5981,3,3,5987,3,3,3,3,3,3,3,3,3,6007,3,6011,
3,3,3,3,3,3,3,3,6029,3,3,3,6037,3,3,6043,3,6047,3,3,
6053,3,3,3,3,3,3,6067,3,3,6073,3,3,6079,3,3,3,3,
6089,6091,3,3,3,3,6101,3,3,3,3,3,6113,3,3,3,6121,3,3,
3,3,6131,6133,3,3,3,3,6143,3,3,3,6151,3,3,3,3,3,
6163,3,3,3,3,6173,3,3,3,3,3,3,3,3,3,3,3,6197,6199,3,
6203,3,3,3,6211,3,3,6217,3,6221,3,3,3,6229,3,3,3,3,3,
3,3,3,6247,3,3,3,3,6257,3,3,6263,3,3,6269,6271,3,3,
6277,3,3,3,3,6287,3,3,3,3,3,6299,6301,3,3,3,3,6311,3,
3,6317,3,3,6323,3,3,6329,3,3,3,6337,3,3,6343,3,3,3,
3,6353,3,3,6359,6361,3,3,6367,3,3,6373,3,3,6379,3,3,
3,3,6389,3,3,3,6397,3,3,3,3,3,3,3,3,3,3,3,6421,3,3,
6427,3,3,3,3,3,3,3,3,3,3,6449,6451,3,3,3,3,3,3,3,3,
6469,3,6473,3,3,3,6481,3,3,3,3,6491,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,6521,3,3,3,6529,3,3,3,3,3,3,3,3,6547,3,
6551,6553,3,3,3,3,6563,3,3,6569,6571,3,3,6577,3,
6581,3,3,3,3,3,3,3,3,6599,3,3,3,6607,3,3,3,3,3,6619,
3,3,3,3,3,3,3,3,6637,3,3,3,3,3,3,3,6653,3,3,6659,
6661,3,3,3,3,3,6673,3,3,6679,3,3,3,3,6689,6691,3,3,
3,3,6701,6703,3,3,6709,3,3,3,3,6719,3,3,3,3,3,3,
6733,3,6737,3,3,3,3,3,3,3,3,3,3,3,6761,6763,3,3,3,3,
3,3,3,6779,6781,3,3,3,3,6791,6793,3,3,3,3,6803,3,3,
3,3,3,3,3,3,3,6823,3,6827,6829,3,6833,3,3,3,6841,3,
3,3,3,3,3,3,6857,3,3,6863,3,3,6869,6871,3,3,3,3,3,
6883,3,3,3,3,3,3,3,6899,3,3,3,6907,3,6911,3,3,6917,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,6947,6949,3,3,3,3,6959,
6961,3,3,6967,3,6971,3,3,6977,3,3,6983,3,3,3,6991,3,
3,6997,3,7001,3,3,3,3,3,7013,3,3,7019,3,3,3,7027,3,
3,3,3,3,7039,3,7043,3,3,3,3,3,3,7057,3,3,3,3,3,7069,
3,3,3,3,7079,3,3,3,3,3,3,3,3,3,3,3,7103,3,3,7109,3,3,
3,3,3,7121,3,3,7127,7129,3,3,3,3,3,3,3,3,3,3,7151,3,
3,3,7159,3,3,3,3,3,3,3,3,7177,3,3,3,3,7187,3,3,7193,
3,3,3,3,3,3,7207,3,7211,7213,3,3,7219,3,3,3,3,7229,3,
3,3,7237,3,3,7243,3,7247,3,3,7253,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,7283,3,3,3,3,3,3,7297,3,3,3,3,7307,7309,3,
3,3,3,3,7321,3,3,3,3,7331,7333,3,3,3,3,3,3,3,7349,
7351,3,3,3,3,3,3,3,3,7369,3,3,3,3,3,3,3,3,3,3,3,7393,
3,3,3,3,3,3,3,3,7411,3,3,7417,3,3,3,3,3,3,3,7433,3,3,3,
3,3,3,3,3,7451,3,3,7457,7459,3,3,3,3,3,3,3,3,7477,3,
7481,3,3,7487,7489,3,3,3,3,7499,3,3,3,7507,3,3,3,3,
7517,3,3,7523,3,3,7529,3,3,3,7537,3,7541,3,3,7547,
7549,3,3,3,3,7559,7561,3,3,3,3,3,7573,3,7577,3,3,
7583,3,3,7589,7591,3,3,3,3,3,7603,3,7607,3,3,3,3,3,
3,7621,3,3,3,3,3,3,3,3,7639,3,7643,3,3,7649,3,3,3,3,
3,3,3,3,3,7669,3,7673,3,3,3,7681,3,3,7687,3,7691,3,
3,3,7699,3,7703,3,3,3,3,3,3,7717,3,3,7723,3,7727,3,
3,3,3,3,3,7741,3,3,3,3,3,7753,3,7757,7759,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,7789,3,7793,3,3,3,3,3,3,3,3,3,3,3,
7817,3,3,7823,3,3,7829,3,3,3,3,3,7841,3,3,3,3,3,
7853,3,3,3,3,3,3,7867,3,3,7873,3,7877,7879,3,7883,3,
3,3,3,3,3,3,3,7901,3,3,7907,3,3,3,3,3,7919,3,3,3,
7927,3,3,7933,3,7937,3,3,3,3,3,7949,7951,3,3,3,3,3,
7963,3,3,3,3,3,3,3,3,3,3,3,3,3,3,7993,3,3,3,3,3,3,3,
8009,8011,3,3,8017,3,3,3,3,3,3,3,3,3,3,8039,3,3,3,3,3,
3,8053,3,3,8059,3,3,3,3,8069,3,3,3,3,3,8081,3,3,
8087,8089,3,8093,3,3,3,8101,3,3,3,3,8111,3,3,8117,3,
3,8123,3,3,3,3,3,3,3,3,3,3,3,8147,3,3,3,3,3,3,8161,3,
3,8167,3,8171,3,3,3,8179,3,3,3,3,3,8191,3,3,3,3,3,3,
3,3,8209,3,3,3,3,8219,8221,3,3,3,3,8231,8233,3,8237,
3,3,8243,3,3,3,3,3,3,3,3,3,8263,3,3,8269,3,8273,3,3,
3,3,3,3,8287,3,8291,8293,3,8297,3,3,3,3,3,3,8311,3,3,
8317,3,3,3,3,3,8329,3,3,3,3,3,3,3,3,3,3,3,8353,3,3,3,
3,8363,3,3,8369,3,3,3,8377,3,3,3,3,8387,8389,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,8419,3,8423,3,3,8429,8431,3,3,
3,3,3,8443,3,8447,3,3,3,3,3,3,8461,3,3,8467,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,8501,3,3,3,3,3,8513,3,3,3,
8521,3,3,8527,3,3,3,3,8537,8539,3,8543,3,3,3,3,3,3,
3,3,3,8563,3,3,3,3,8573,3,3,3,8581,3,3,3,3,3,3,3,
8597,8599,3,3,3,3,8609,3,3,3,3,3,3,8623,3,8627,8629,
3,3,3,3,3,8641,3,3,8647,3,3,3,3,3,3,3,8663,3,3,8669,
3,3,3,8677,3,8681,3,3,3,8689,3,8693,3,3,8699,3,3,3,
8707,3,3,8713,3,3,8719,3,3,3,3,3,8731,3,3,8737,3,
8741,3,3,8747,3,3,8753,3,3,3,8761,3,3,3,3,3,3,3,3,
8779,3,8783,3,3,3,3,3,3,3,3,3,8803,3,8807,3,3,3,3,3,
8819,8821,3,3,3,3,8831,3,3,8837,8839,3,3,3,3,8849,3,
3,3,3,3,8861,8863,3,8867,3,3,3,3,3,3,3,3,3,8887,3,3,
8893,3,3,3,3,3,3,3,3,3,3,3,3,3,3,8923,3,3,8929,3,
8933,3,3,3,8941,3,3,3,3,8951,3,3,3,3,3,8963,3,3,
8969,8971,3,3,3,3,3,3,3,3,3,3,3,3,3,8999,9001,3,3,
9007,3,9011,9013,3,3,3,3,3,3,3,9029,3,3,3,3,3,9041,
9043,3,3,9049,3,3,3,3,9059,3,3,3,9067,3,3,3,3,3,3,3,
3,3,3,3,9091,3,3,3,3,3,9103,3,3,9109,3,3,3,3,3,3,3,3,
9127,3,3,9133,3,9137,3,3,3,3,3,3,9151,3,3,9157,3,
9161,3,3,3,3,3,9173,3,3,3,9181,3,3,9187,3,3,3,3,3,
9199,3,9203,3,3,9209,3,3,3,3,3,9221,3,3,9227,3,3,3,
3,3,9239,9241,3,3,3,3,3,3,3,9257,3,3,3,3,3,3,3,3,3,
9277,3,9281,9283,3,3,3,3,9293,3,3,3,3,3,3,3,3,9311,3,
3,3,9319,3,9323,3,3,3,3,3,3,9337,3,9341,9343,3,3,
9349,3,3,3,3,3,3,3,3,3,3,9371,3,3,9377,3,3,3,3,3,3,
9391,3,3,9397,3,3,9403,3,3,3,3,9413,3,3,9419,9421,3,
3,3,3,9431,9433,3,9437,9439,3,3,3,3,3,3,3,3,3,3,
9461,9463,3,9467,3,3,9473,3,3,9479,3,3,3,3,3,9491,3,
3,9497,3,3,3,3,3,3,9511,3,3,3,3,9521,3,3,3,3,3,9533,3,
3,9539,3,3,3,9547,3,9551,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,9587,3,3,3,3,3,3,9601,3,3,3,3,3,9613,3,3,9619,
3,9623,3,3,9629,9631,3,3,3,3,3,9643,3,3,9649,3,3,3,
3,3,9661,3,3,3,3,3,3,3,9677,9679,3,3,3,3,9689,3,3,3,
9697,3,3,3,3,3,3,3,3,3,3,9719,9721,3,3,3,3,3,9733,3,
3,9739,3,9743,3,3,9749,3,3,3,3,3,3,3,3,9767,9769,3,
3,3,3,3,9781,3,3,9787,3,9791,3,3,3,3,3,9803,3,3,3,
9811,3,3,9817,3,3,3,3,3,9829,3,9833,3,3,9839,3,3,3,3,
3,9851,3,3,9857,9859,3,3,3,3,3,9871,3,3,3,3,3,9883,
3,9887,3,3,3,3,3,3,9901,3,3,9907,3,3,3,3,3,3,3,9923,
3,3,9929,9931,3,3,3,3,9941,3,3,3,9949,3,3,3,3,3,3,3,
3,9967,3,3,9973,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,10007,
10009,3,3,3,3,3,3,3,3,3,3,3,3,3,10037,10039,3,3,3,3,
3,3,3,3,3,3,10061,3,3,10067,10069,3,3,3,3,10079,3,3,
3,3,3,10091,10093,3,3,10099,3,10103,3,3,3,10111,3,
3,3,3,3,3,3,3,3,3,10133,3,3,10139,10141,3,3,3,3,
10151,3,3,3,10159,3,10163,3,3,10169,3,3,3,10177,3,
10181,3,3,3,3,3,10193,3,3,3,3,3,3,3,3,10211,3,3,3,3,3,
10223,3,3,3,3,3,3,3,3,3,10243,3,10247,3,3,10253,3,3,
10259,3,3,3,10267,3,10271,10273,3,3,3,3,3,3,3,
10289,3,3,3,3,3,10301,10303,3,3,3,3,10313,3,3,3,
10321,3,3,3,3,10331,10333,3,10337,3,3,10343,3,3,3,
3,3,3,10357,3,3,3,3,3,10369,3,3,3,3,3,3,3,3,3,3,
10391,3,3,3,10399,3,3,3,3,3,3,3,3,3,3,3,3,3,10427,
10429,3,10433,3,3,3,3,3,3,3,3,3,10453,3,10457,
10459,3,10463,3,3,3,3,3,3,10477,3,3,3,3,10487,3,3,3,
3,3,10499,10501,3,3,3,3,3,10513,3,3,3,3,3,3,3,10529,
10531,3,3,3,3,3,3,3,3,3,3,3,3,3,10559,3,3,3,10567,3,
3,3,3,3,3,3,3,3,3,10589,3,3,3,10597,3,10601,3,3,
10607,3,3,10613,3,3,3,3,3,3,10627,3,10631,3,3,3,
10639,3,3,3,3,3,10651,3,3,10657,3,3,10663,3,10667,
3,3,3,3,3,3,3,3,3,10687,3,10691,3,3,3,3,3,3,3,3,
10709,10711,3,3,3,3,3,10723,3,3,10729,3,10733,3,3,
10739,3,3,3,3,3,3,10753,3,3,3,3,3,3,3,3,10771,3,3,3,
3,10781,3,3,3,10789,3,3,3,3,10799,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,10831,3,3,10837,3,3,3,3,10847,3,3,10853,
3,3,10859,10861,3,3,10867,3,3,3,3,3,3,3,10883,3,3,
10889,10891,3,3,3,3,3,10903,3,3,10909,3,3,3,3,3,3,3,
3,3,3,3,3,3,10937,10939,3,3,3,3,10949,3,3,3,10957,3,
3,3,3,3,3,3,10973,3,3,10979,3,3,3,10987,3,3,10993,3,
3,3,3,11003,3,3,3,3,3,3,3,3,3,3,3,11027,3,3,3,3,3,3,3,
3,3,11047,3,3,3,3,11057,11059,3,3,3,3,11069,11071,3,
3,3,3,3,11083,3,11087,3,3,11093,3,3,3,3,3,3,3,3,3,
11113,3,11117,11119,3,3,3,3,3,11131,3,3,3,3,3,3,3,3,
11149,3,3,3,3,11159,11161,3,3,3,3,11171,11173,3,
11177,3,3,3,3,3,3,3,3,3,11197,3,3,3,3,3,3,3,11213,3,3,
3,3,3,3,3,3,3,3,3,3,11239,3,11243,3,3,3,11251,3,3,
11257,3,11261,3,3,3,3,3,11273,3,3,11279,3,3,3,11287,
3,3,3,3,3,11299,3,3,3,3,3,11311,3,3,11317,3,11321,3,
3,3,11329,3,3,3,3,3,3,3,3,3,3,11351,11353,3,3,3,3,3,3,
3,11369,3,3,3,3,3,3,11383,3,3,3,3,11393,3,3,11399,3,
3,3,3,3,11411,3,3,3,3,3,11423,3,3,3,3,3,3,11437,3,3,
11443,3,11447,3,3,3,3,3,3,3,3,3,11467,3,11471,3,3,3,
3,3,11483,3,3,11489,11491,3,3,11497,3,3,11503,3,3,3,
3,3,3,3,11519,3,3,3,11527,3,3,3,3,3,3,3,3,3,3,11549,
11551,3,3,3,3,3,3,3,3,3,3,3,3,3,11579,3,3,3,11587,3,3,
11593,3,11597,3,3,3,3,3,3,3,3,3,11617,3,11621,3,3,3,
3,3,11633,3,3,3,3,3,3,3,3,3,3,3,11657,3,3,3,3,3,3,3,3,
3,11677,3,11681,3,3,3,11689,3,3,3,3,11699,11701,3,3,
3,3,3,3,3,11717,11719,3,3,3,3,3,11731,3,3,3,3,3,
11743,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,11777,11779,3,
11783,3,3,11789,3,3,3,3,3,11801,3,3,11807,3,3,11813,
3,3,3,11821,3,3,11827,3,11831,11833,3,3,11839,3,3,3,
3,3,3,3,3,3,3,3,11863,3,11867,3,3,3,3,3,3,3,3,3,11887,
3,3,3,3,11897,3,3,11903,3,3,11909,3,3,3,3,3,3,11923,
3,11927,3,3,11933,3,3,11939,11941,3,3,3,3,3,11953,3,
3,11959,3,3,3,3,11969,11971,3,3,3,3,11981,3,3,11987,
3,3,3,3,3,3,3,3,3,12007,3,12011,3,3,3,3,3,3,3,3,3,3,3,
3,12037,3,12041,12043,3,3,12049,3,3,3,3,3,3,3,3,3,3,
12071,12073,3,3,3,3,3,3,3,3,3,3,3,12097,3,12101,3,3,
12107,12109,3,12113,3,3,12119,3,3,3,3,3,3,3,3,3,3,3,
12143,3,3,12149,3,3,3,12157,3,12161,12163,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,12197,3,3,12203,3,3,3,12211,3,
3,3,3,3,3,3,12227,3,3,3,3,3,12239,12241,3,3,3,3,
12251,12253,3,3,3,3,12263,3,3,12269,3,3,3,12277,3,
12281,3,3,3,12289,3,3,3,3,3,12301,3,3,3,3,3,3,3,3,3,
3,12323,3,3,12329,3,3,3,3,3,3,12343,3,12347,3,3,3,3,
3,3,3,3,3,3,3,3,12373,3,12377,12379,3,3,3,3,3,12391,
3,3,3,3,12401,3,3,3,12409,3,12413,3,3,3,12421,3,3,3,
3,3,12433,3,12437,3,3,3,3,3,3,12451,3,3,12457,3,3,3,
3,3,3,3,12473,3,3,12479,3,3,3,12487,3,12491,3,3,
12497,3,3,12503,3,3,3,12511,3,3,12517,3,3,3,3,
12527,3,3,3,3,3,12539,12541,3,3,12547,3,3,12553,3,
3,3,3,3,3,3,12569,3,3,3,12577,3,3,12583,3,3,12589,3,
3,3,3,3,12601,3,3,3,3,12611,12613,3,3,12619,3,3,3,3,
3,3,3,3,12637,3,12641,3,3,12647,3,3,12653,3,3,
12659,3,3,3,3,3,12671,3,3,3,3,3,3,3,3,12689,3,3,3,
12697,3,3,12703,3,3,3,3,12713,3,3,3,12721,3,3,3,3,3,
3,3,3,12739,3,12743,3,3,3,3,3,3,12757,3,3,12763,3,3,
3,3,3,3,3,3,12781,3,3,3,3,12791,3,3,3,12799,3,3,3,3,
12809,3,3,3,3,3,12821,12823,3,3,12829,3,3,3,3,3,
12841,3,3,3,3,3,12853,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,12889,3,12893,3,3,12899,3,3,3,12907,3,12911,3,3,
12917,12919,3,12923,3,3,3,3,3,3,3,3,12941,3,3,3,3,3,
12953,3,3,12959,3,3,3,12967,3,3,12973,3,3,12979,3,
12983,3,3,3,3,3,3,3,3,13001,13003,3,13007,13009,3,
3,3,3,3,3,3,3,3,3,3,13033,3,13037,3,3,13043,3,3,
13049,3,3,3,3,3,3,13063,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
13093,3,3,13099,3,13103,3,3,13109,3,3,3,3,3,13121,
3,3,13127,3,3,3,3,3,3,3,3,3,13147,3,13151,3,3,3,
13159,3,13163,3,3,3,13171,3,3,13177,3,3,13183,3,
13187,3,3,3,3,3,3,3,3,3,3,3,3,3,3,13217,13219,3,3,3,
3,13229,3,3,3,3,3,13241,3,3,3,13249,3,3,3,3,13259,3,
3,3,13267,3,3,3,3,3,3,3,3,3,3,3,13291,3,3,13297,3,3,
3,3,3,13309,3,13313,3,3,3,3,3,3,13327,3,13331,3,3,
13337,13339,3,3,3,3,3,3,3,3,3,3,3,3,3,13367,3,3,3,3,
3,3,13381,3,3,3,3,3,3,3,13397,13399,3,3,3,3,3,13411,
3,3,13417,3,13421,3,3,3,3,3,3,3,3,3,13441,3,3,3,3,
13451,3,3,13457,3,3,13463,3,3,13469,3,3,3,13477,3,
3,3,3,13487,3,3,3,3,3,13499,3,3,3,3,3,3,13513,3,3,3,
3,13523,3,3,3,3,3,3,13537,3,3,3,3,3,3,3,13553,3,3,3,
3,3,3,13567,3,3,3,3,13577,3,3,3,3,3,3,13591,3,3,
13597,3,3,3,3,3,3,3,13613,3,3,13619,3,3,3,13627,3,3,
13633,3,3,3,3,3,3,3,13649,3,3,3,3,3,3,3,3,3,13669,3,
3,3,3,13679,13681,3,3,13687,3,13691,13693,3,13697,
3,3,3,3,3,13709,13711,3,3,3,3,13721,13723,3,3,
13729,3,3,3,3,3,3,3,3,3,3,13751,3,3,13757,13759,3,
13763,3,3,3,3,3,3,3,3,13781,3,3,3,13789,3,3,3,3,
13799,3,3,3,13807,3,3,3,3,3,3,3,3,3,3,13829,13831,3,
3,3,3,13841,3,3,3,3,3,3,3,3,13859,3,3,3,3,3,3,13873,
3,13877,13879,3,13883,3,3,3,3,3,3,3,3,13901,13903,
3,13907,3,3,13913,3,3,3,13921,3,3,3,3,13931,13933,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,13963,3,13967,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,13997,13999,3,3,3,3,14009,14011,3,3,
3,3,3,3,3,3,14029,3,14033,3,3,3,3,3,3,3,3,14051,3,3,
14057,3,3,3,3,3,3,14071,3,3,3,3,14081,14083,3,
14087,3,3,3,3,3,3,3,3,3,14107,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,14143,3,3,14149,3,14153,3,3,14159,3,3,3,3,
3,3,14173,3,14177,3,3,3,3,3,3,3,3,3,14197,3,3,3,3,
14207,3,3,3,3,3,3,14221,3,3,3,3,3,3,3,3,3,3,14243,3,
3,14249,14251,3,3,3,3,3,3,3,3,3,3,3,3,3,3,14281,3,3,
3,3,3,14293,3,3,3,3,14303,3,3,3,3,3,3,3,3,14321,
14323,3,14327,3,3,3,3,3,3,14341,3,3,14347,3,3,3,3,3,
3,3,3,3,3,14369,3,3,3,3,3,3,3,3,14387,14389,3,3,3,3,3,
14401,3,3,14407,3,14411,3,3,3,14419,3,14423,3,3,3,
14431,3,3,14437,3,3,3,3,14447,14449,3,3,3,3,3,14461,
3,3,3,3,3,3,3,3,14479,3,3,3,3,14489,3,3,3,3,3,3,14503,
3,3,3,3,3,3,3,14519,3,3,3,3,3,3,14533,3,14537,3,3,
14543,3,3,14549,14551,3,3,14557,3,14561,14563,3,3,
3,3,3,3,3,3,3,3,3,3,3,14591,14593,3,3,3,3,3,3,3,3,3,3,3,
3,3,14621,3,3,14627,14629,3,14633,3,3,14639,3,3,3,3,
3,3,14653,3,14657,3,3,3,3,3,14669,3,3,3,3,3,3,14683,
3,3,3,3,3,3,3,14699,3,3,3,3,3,3,14713,3,14717,3,3,
14723,3,3,3,14731,3,3,14737,3,14741,3,3,14747,3,3,
14753,3,3,14759,3,3,3,14767,3,14771,3,3,3,14779,3,
14783,3,3,3,3,3,3,14797,3,3,3,3,3,3,3,14813,3,3,3,
14821,3,3,14827,3,14831,3,3,3,3,3,14843,3,3,3,14851,
3,3,3,3,3,3,3,14867,14869,3,3,3,3,14879,3,3,3,14887,
3,14891,3,3,14897,3,3,3,3,3,3,3,3,3,3,3,3,14923,3,3,
14929,3,3,3,3,14939,3,3,3,14947,3,14951,3,3,14957,3,
3,3,3,3,14969,3,3,3,3,3,3,14983,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,15013,3,15017,3,3,3,3,3,3,15031,3,3,3,3,3,3,3,3,3,
3,15053,3,3,3,15061,3,3,3,3,3,15073,3,15077,3,3,
15083,3,3,3,15091,3,3,3,3,15101,3,3,15107,3,3,3,3,3,
3,15121,3,3,3,3,15131,3,3,15137,15139,3,3,3,3,15149,
3,3,3,3,3,15161,3,3,3,3,3,15173,3,3,3,3,3,3,15187,3,3,
15193,3,3,15199,3,3,3,3,3,3,3,3,15217,3,3,3,3,15227,
3,3,15233,3,3,3,15241,3,3,3,3,3,3,3,3,15259,3,15263,
3,3,15269,15271,3,3,15277,3,3,3,3,15287,15289,3,3,3,
3,15299,3,3,3,15307,3,3,15313,3,3,15319,3,3,3,3,
15329,15331,3,3,3,3,3,3,3,3,15349,3,3,3,3,15359,
15361,3,3,3,3,3,15373,3,15377,3,3,15383,3,3,3,15391,
3,3,3,3,15401,3,3,3,3,3,15413,3,3,3,3,3,3,15427,3,3,3,
3,3,15439,3,15443,3,3,3,15451,3,3,3,3,15461,3,3,
15467,3,3,15473,3,3,3,3,3,3,3,3,3,15493,3,15497,3,3,
3,3,3,3,15511,3,3,3,3,3,3,3,15527,3,3,3,3,3,3,15541,3,
3,3,3,15551,3,3,3,15559,3,3,3,3,15569,3,3,3,3,3,
15581,15583,3,3,3,3,3,3,3,3,15601,3,3,15607,3,3,3,3,
3,15619,3,3,3,3,15629,3,3,3,3,3,15641,15643,3,15647,
15649,3,3,3,3,3,15661,3,3,15667,3,15671,3,3,3,15679,
3,15683,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,15727,
3,15731,15733,3,15737,15739,3,3,3,3,15749,3,3,3,3,3,
15761,3,3,15767,3,3,15773,3,3,3,3,3,3,15787,3,15791,
3,3,15797,3,3,15803,3,3,15809,3,3,3,15817,3,3,15823,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,15859,3,3,3,3,3,3,3,3,
15877,3,15881,3,3,15887,15889,3,3,3,3,3,15901,3,3,
15907,3,3,15913,3,3,15919,3,15923,3,3,3,3,3,3,15937,
3,3,3,3,3,3,3,3,3,3,15959,3,3,3,3,3,15971,15973,3,3,3,
3,3,3,3,3,15991,3,3,3,3,16001,3,3,16007,3,3,3,3,3,3,3,
3,3,3,3,3,16033,3,3,3,3,3,3,3,3,3,3,3,16057,3,16061,
16063,3,16067,16069,3,16073,3,3,3,3,3,3,16087,3,
16091,3,3,16097,3,3,16103,3,3,3,16111,3,3,3,3,3,3,3,
16127,3,3,3,3,3,16139,16141,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,16183,3,16187,16189,3,16193,3,3,3,3,3,
3,3,3,3,3,3,16217,3,3,16223,3,3,16229,16231,3,3,3,3,
3,3,3,3,16249,3,16253,3,3,3,3,3,3,16267,3,3,16273,3,
3,3,3,3,3,3,3,3,3,3,3,3,16301,3,3,3,3,3,3,3,3,16319,3,3,
3,3,3,3,16333,3,3,16339,3,3,3,3,16349,3,3,3,3,3,
16361,16363,3,3,16369,3,3,3,3,3,16381,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,16411,3,3,16417,3,16421,3,3,16427,3,3,
16433,3,3,3,3,3,3,16447,3,16451,16453,3,3,3,3,3,3,3,
3,3,3,3,16477,3,16481,3,3,16487,3,3,16493,3,3,3,3,3,
3,3,3,3,3,3,3,16519,3,3,3,3,16529,3,3,3,3,3,3,3,3,
16547,3,3,16553,3,3,3,16561,3,3,16567,3,3,16573,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,16603,3,16607,3,3,3,3,3,16619,
3,3,3,3,3,16631,16633,3,3,3,3,3,3,3,16649,16651,3,3,
16657,3,16661,3,3,3,3,3,16673,3,3,3,3,3,3,3,3,16691,
16693,3,3,16699,3,16703,3,3,3,3,3,3,3,3,3,3,3,3,
16729,3,3,3,3,3,16741,3,3,16747,3,3,3,3,3,16759,3,
16763,3,3,3,3,3,3,3,3,3,3,3,16787,3,3,3,3,3,3,3,3,3,3,3,
16811,3,3,3,3,3,16823,3,3,16829,16831,3,3,3,3,3,
16843,3,3,3,3,3,3,3,3,3,3,3,3,3,16871,3,3,3,16879,3,
16883,3,3,16889,3,3,3,3,3,16901,16903,3,3,3,3,3,3,3,
3,16921,3,3,16927,3,16931,3,3,16937,3,3,16943,3,3,3,
3,3,3,3,3,3,16963,3,3,3,3,3,3,3,16979,16981,3,3,
16987,3,3,16993,3,3,3,3,3,3,3,3,17011,3,3,3,3,17021,3,
3,17027,17029,3,17033,3,3,3,17041,3,3,17047,3,3,
17053,3,3,3,3,3,3,3,3,3,3,3,17077,3,3,3,3,3,3,3,17093,
3,3,17099,3,3,3,17107,3,3,3,3,17117,3,3,17123,3,3,3,3,
3,3,17137,3,3,3,3,3,3,3,3,3,3,17159,3,3,3,17167,3,3,3,
3,3,3,3,17183,3,3,17189,17191,3,3,3,3,3,17203,3,
17207,17209,3,3,3,3,3,3,3,3,3,3,17231,3,3,3,17239,3,
3,3,3,3,3,3,3,17257,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
17291,17293,3,3,17299,3,3,3,3,3,3,3,3,17317,3,17321,
3,3,17327,3,3,17333,3,3,3,17341,3,3,3,3,17351,3,3,3,
17359,3,3,3,3,3,3,3,3,17377,3,3,17383,3,17387,17389,
3,17393,3,3,3,17401,3,3,3,3,3,3,3,17417,17419,3,3,3,
3,3,17431,3,3,3,3,3,17443,3,3,17449,3,3,3,3,3,3,3,3,
17467,3,17471,3,3,17477,3,3,17483,3,3,17489,17491,
3,3,17497,3,3,3,3,3,17509,3,3,3,3,17519,3,3,3,3,3,3,3,
3,3,17539,3,3,3,3,3,17551,3,3,3,3,3,3,3,3,17569,3,
17573,3,3,17579,17581,3,3,3,3,3,3,3,17597,17599,3,3,
3,3,17609,3,3,3,3,3,3,17623,3,17627,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,17657,17659,3,3,3,3,17669,3,3,3,3,3,17681,
17683,3,3,3,3,3,3,3,3,3,3,3,17707,3,3,17713,3,3,3,3,3,
3,3,17729,3,3,3,17737,3,3,3,3,17747,17749,3,3,3,3,3,
17761,3,3,3,3,3,3,3,3,3,3,17783,3,3,17789,17791,3,3,
3,3,3,3,3,17807,3,3,3,3,3,3,3,3,3,17827,3,3,3,3,17837,
17839,3,3,3,3,3,17851,3,3,3,3,3,17863,3,3,3,3,3,3,3,3,
17881,3,3,3,3,17891,3,3,3,3,3,17903,3,3,17909,17911,
3,3,3,3,17921,17923,3,3,17929,3,3,3,3,17939,3,3,3,3,
3,3,3,3,17957,17959,3,3,3,3,3,17971,3,3,17977,3,
17981,3,3,17987,17989,3,3,3,3,3,3,3,3,3,3,3,18013,3,
3,3,3,3,3,3,3,3,3,3,3,3,18041,18043,3,18047,18049,3,
3,3,3,18059,18061,3,3,3,3,3,3,3,18077,3,3,3,3,3,
18089,3,3,3,18097,3,3,3,3,3,3,3,3,3,3,18119,18121,3,3,
18127,3,18131,18133,3,3,3,3,18143,3,3,18149,3,3,3,3,
3,3,3,3,3,18169,3,3,3,3,3,18181,3,3,3,3,18191,3,3,3,
18199,3,3,3,3,3,18211,3,3,18217,3,3,18223,3,3,18229,
3,18233,3,3,3,3,3,3,3,3,18251,18253,3,18257,3,3,3,3,
3,18269,3,3,3,3,3,3,3,3,18287,18289,3,3,3,3,3,18301,
3,3,18307,3,18311,18313,3,3,3,3,3,3,3,18329,3,3,3,3,3,
18341,3,3,3,3,3,18353,3,3,3,3,3,3,18367,3,18371,3,3,
3,18379,3,3,3,3,3,3,3,3,18397,3,18401,3,3,3,3,3,
18413,3,3,3,3,3,3,18427,3,3,18433,3,3,18439,3,18443,
3,3,3,18451,3,3,18457,3,18461,3,3,3,3,3,3,3,3,3,
18481,3,3,3,3,3,18493,3,3,3,3,18503,3,3,3,3,3,3,
18517,3,18521,18523,3,3,3,3,3,3,3,18539,18541,3,3,3,
3,3,18553,3,3,3,3,3,3,3,3,3,3,3,3,3,3,18583,3,18587,3,
3,18593,3,3,3,3,3,3,3,3,3,3,3,18617,3,3,3,3,3,3,3,3,3,
18637,3,3,3,3,3,3,3,3,3,3,3,18661,3,3,3,3,18671,3,3,3,
18679,3,3,3,3,3,18691,3,3,3,3,18701,3,3,3,3,3,18713,
3,3,18719,3,3,3,3,3,18731,3,3,3,3,3,18743,3,3,18749,
3,3,3,18757,3,3,3,3,3,3,3,18773,3,3,3,3,3,3,18787,3,3,
18793,3,18797,3,3,18803,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,18839,3,3,3,3,3,3,3,3,3,18859,3,3,3,3,18869,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,18899,3,3,3,3,3,18911,18913,3,
18917,18919,3,3,3,3,3,3,3,3,3,3,3,3,3,18947,3,3,3,3,3,
18959,3,3,3,3,3,3,18973,3,3,18979,3,3,3,3,3,3,3,3,3,3,
19001,3,3,3,19009,3,19013,3,3,3,3,3,3,3,3,19031,3,3,
19037,3,3,3,3,3,3,19051,3,3,3,3,3,3,3,3,19069,3,
19073,3,3,19079,19081,3,3,19087,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,19121,3,3,3,3,3,3,3,3,19139,19141,3,3,3,3,
3,3,3,19157,3,3,19163,3,3,3,3,3,3,3,3,19181,19183,3,
3,3,3,3,3,3,3,3,3,3,19207,3,19211,19213,3,3,19219,3,3,
3,3,3,19231,3,3,19237,3,3,3,3,3,19249,3,3,3,3,19259,
3,3,3,19267,3,3,19273,3,3,3,3,3,3,3,19289,3,3,3,3,3,
19301,3,3,3,19309,3,3,3,3,19319,3,3,3,3,3,3,19333,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,19373,3,3,19379,
19381,3,3,19387,3,19391,3,3,3,3,3,19403,3,3,3,3,3,3,
19417,3,19421,19423,3,19427,19429,3,19433,3,3,3,
19441,3,3,19447,3,3,3,3,19457,3,3,19463,3,3,19469,
19471,3,3,19477,3,3,19483,3,3,19489,3,3,3,3,3,19501,
3,3,19507,3,3,3,3,3,3,3,3,3,3,3,19531,3,3,3,3,19541,
19543,3,3,3,3,19553,3,3,19559,3,3,3,3,3,19571,3,3,
19577,3,3,19583,3,3,3,3,3,3,19597,3,3,19603,3,3,
19609,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
19661,3,3,3,3,3,3,3,3,3,19681,3,3,19687,3,3,3,3,
19697,19699,3,3,3,3,19709,3,3,3,19717,3,3,3,3,19727,
3,3,3,3,3,19739,3,3,3,3,3,19751,19753,3,3,19759,3,
19763,3,3,3,3,3,3,19777,3,3,3,3,3,3,3,19793,3,3,3,
19801,3,3,3,3,3,19813,3,3,19819,3,3,3,3,3,3,3,3,3,3,
19841,19843,3,3,3,3,19853,3,3,3,19861,3,3,19867,3,3,
3,3,3,3,3,3,3,3,19889,19891,3,3,3,3,3,3,3,3,3,3,19913,
3,3,19919,3,3,3,19927,3,3,3,3,19937,3,3,3,3,3,19949,
3,3,3,3,3,19961,19963,3,3,3,3,19973,3,3,19979,3,3,3,
3,3,19991,19993,3,19997,3,3,3,3,3,3,20011,3,3,3,3,
20021,20023,3,3,20029,3,3,3,3,3,3,3,3,20047,3,20051,
3,3,3,3,3,20063,3,3,3,20071,3,3,3,3,3,3,3,3,20089,3,3,
3,3,3,20101,3,3,20107,3,3,20113,3,20117,3,3,20123,3,
3,20129,3,3,3,3,3,3,20143,3,20147,20149,3,3,3,3,3,
20161,3,3,3,3,3,20173,3,20177,3,3,20183,3,3,3,3,3,3,
3,3,20201,3,3,3,3,3,3,3,3,20219,3,3,3,3,3,20231,
20233,3,3,3,3,3,3,3,20249,3,3,3,3,3,20261,3,3,3,
20269,3,3,3,3,3,3,3,3,20287,3,3,3,3,20297,3,3,3,3,3,3,
3,3,3,3,3,3,20323,3,20327,3,3,20333,3,3,3,20341,3,3,
20347,3,3,20353,3,20357,20359,3,3,3,3,20369,3,3,3,3,
3,3,3,3,3,20389,3,20393,3,3,20399,3,3,3,20407,3,
20411,3,3,3,3,3,3,3,3,3,20431,3,3,3,3,20441,20443,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,20477,20479,3,20483,3,3,3,
3,3,3,3,3,3,3,3,20507,20509,3,3,3,3,3,20521,3,3,3,3,3,
20533,3,3,3,3,20543,3,3,20549,20551,3,3,3,3,3,20563,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,20593,3,3,20599,3,3,3,3,3,
20611,3,3,3,3,3,3,3,20627,3,3,3,3,3,20639,20641,3,3,3,
3,3,3,3,3,3,3,20663,3,3,3,3,3,3,3,3,20681,3,3,3,3,3,
20693,3,3,3,3,3,3,20707,3,3,3,3,20717,20719,3,3,3,3,
3,20731,3,3,3,3,3,20743,3,20747,20749,3,20753,3,3,
20759,3,3,3,3,3,20771,20773,3,3,3,3,3,3,3,20789,3,3,
3,3,3,3,3,3,20807,20809,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,20849,3,3,3,20857,3,3,3,3,3,3,3,20873,3,3,
20879,3,3,3,20887,3,3,3,3,20897,20899,3,20903,3,3,3,
3,3,3,3,3,20921,3,3,3,20929,3,3,3,3,20939,3,3,3,
20947,3,3,3,3,3,20959,3,20963,3,3,3,3,3,3,3,3,20981,
20983,3,3,3,3,3,3,3,3,21001,3,3,3,3,21011,21013,3,
21017,21019,3,21023,3,3,3,21031,3,3,3,3,3,3,3,3,3,3,
3,3,3,21059,21061,3,3,21067,3,3,3,3,3,3,3,3,3,3,
21089,3,3,3,3,3,21101,3,3,21107,3,3,3,3,3,3,21121,3,3,
3,3,3,3,3,3,21139,3,21143,3,3,21149,3,3,3,21157,3,3,
21163,3,3,21169,3,3,3,3,21179,3,3,3,21187,3,21191,
21193,3,3,3,3,3,3,3,3,21211,3,3,3,3,21221,3,3,21227,3,
3,3,3,3,3,3,3,3,21247,3,3,3,3,3,3,3,3,3,3,21269,3,3,3,
21277,3,3,21283,3,3,3,3,3,3,3,3,3,3,3,3,3,3,21313,3,
21317,21319,3,21323,3,3,3,3,3,3,3,3,21341,3,3,21347,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,21377,21379,3,21383,3,3,3,
21391,3,3,21397,3,21401,3,3,21407,3,3,3,3,3,21419,3,
3,3,3,3,3,21433,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,21467,3,
3,3,3,3,3,21481,3,3,21487,3,21491,21493,3,3,21499,3,
21503,3,3,3,3,3,3,21517,3,21521,21523,3,3,21529,3,3,
3,3,3,3,3,3,3,3,3,3,3,21557,21559,3,21563,3,3,21569,
3,3,3,21577,3,3,3,3,21587,21589,3,3,3,3,21599,21601,
3,3,3,3,21611,21613,3,21617,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,21647,21649,3,3,3,3,3,21661,3,3,3,3,3,21673,3,3,3,
3,21683,3,3,3,3,3,3,3,3,21701,3,3,3,3,3,21713,3,3,3,3,
3,3,21727,3,3,3,3,21737,21739,3,3,3,3,3,21751,3,3,
21757,3,3,3,3,21767,3,3,21773,3,3,3,3,3,3,21787,3,3,
3,3,3,21799,3,21803,3,3,3,3,3,3,21817,3,21821,3,3,3,
3,3,3,3,3,21839,21841,3,3,3,3,21851,3,3,3,21859,3,
21863,3,3,3,21871,3,3,3,3,21881,3,3,3,3,3,21893,3,3,
3,3,3,3,3,3,21911,3,3,3,3,3,3,3,3,21929,3,3,3,21937,3,
3,21943,3,3,3,3,3,3,3,3,21961,3,3,3,3,3,3,3,21977,3,3,
3,3,3,3,21991,3,3,21997,3,3,22003,3,3,3,3,22013,3,3,
3,3,3,3,22027,3,22031,3,3,22037,22039,3,3,3,3,3,
22051,3,3,3,3,3,22063,3,22067,3,3,22073,3,3,22079,3,
3,3,3,3,22091,22093,3,3,3,3,3,3,3,22109,22111,3,3,3,3,
3,22123,3,3,22129,3,22133,3,3,3,3,3,3,22147,3,3,
22153,3,22157,22159,3,3,3,3,3,22171,3,3,3,3,3,3,3,3,
22189,3,22193,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22229,
3,3,3,3,3,3,3,3,22247,3,3,3,3,3,22259,3,3,3,3,3,22271,
22273,3,22277,22279,3,22283,3,3,3,22291,3,3,3,3,3,
22303,3,22307,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22343,
3,3,22349,3,3,3,3,3,3,3,3,22367,22369,3,3,3,3,3,
22381,3,3,3,3,22391,3,3,22397,3,3,3,3,3,22409,3,3,3,
3,3,3,3,3,3,3,3,22433,3,3,3,22441,3,3,22447,3,3,
22453,3,3,3,3,3,3,3,22469,3,3,3,3,3,22481,22483,3,3,
3,3,3,3,3,3,22501,3,3,3,3,22511,3,3,3,3,3,3,3,3,3,
22531,3,3,3,3,22541,22543,3,3,22549,3,3,3,3,3,3,3,3,
22567,3,22571,22573,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,22613,3,3,22619,22621,3,3,3,3,3,3,3,22637,22639,
3,22643,3,3,3,22651,3,3,3,3,3,3,3,3,22669,3,3,3,3,
22679,3,3,3,3,3,22691,3,3,22697,22699,3,3,3,3,22709,
3,3,3,22717,3,22721,3,3,22727,3,3,3,3,3,22739,22741,
3,3,3,3,22751,3,3,3,3,3,3,3,3,22769,3,3,3,22777,3,3,
22783,3,22787,3,3,3,3,3,3,3,3,3,22807,3,22811,3,3,
22817,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,22853,3,3,
22859,22861,3,3,3,3,22871,3,3,22877,3,3,3,3,3,3,3,3,
3,3,3,22901,3,3,22907,3,3,3,3,3,3,22921,3,3,3,3,3,3,3,
22937,3,3,22943,3,3,3,3,3,3,3,3,22961,22963,3,3,3,3,
22973,3,3,3,3,3,3,3,3,3,22993,3,3,3,3,23003,3,3,3,
23011,3,3,23017,3,23021,3,3,23027,23029,3,3,3,3,
23039,23041,3,3,3,3,3,23053,3,23057,23059,3,23063,
3,3,3,23071,3,3,3,3,23081,3,3,23087,3,3,3,3,3,23099,
3,3,3,3,3,3,3,3,23117,3,3,3,3,3,3,23131,3,3,3,3,3,
23143,3,3,3,3,3,3,3,23159,3,3,3,23167,3,3,23173,3,3,
3,3,3,3,3,23189,3,3,3,23197,3,23201,23203,3,3,23209,
3,3,3,3,3,3,3,3,23227,3,3,3,3,3,3,3,3,3,3,3,23251,3,3,3,
3,3,3,3,3,23269,3,3,3,3,23279,3,3,3,3,3,23291,23293,
3,23297,3,3,3,3,3,3,23311,3,3,3,3,23321,3,3,23327,3,3,
23333,3,3,23339,3,3,3,3,3,3,3,3,23357,3,3,3,3,3,
23369,23371,3,3,3,3,3,3,3,3,3,3,3,3,3,23399,3,3,3,3,3,
3,3,3,23417,3,3,3,3,3,3,23431,3,3,3,3,3,3,3,23447,3,3,
3,3,3,23459,3,3,3,3,3,3,23473,3,3,3,3,3,3,3,3,3,3,3,
23497,3,3,3,3,3,23509,3,3,3,3,3,3,3,3,3,3,23531,3,3,
23537,23539,3,3,3,3,23549,3,3,3,23557,3,23561,
23563,3,23567,3,3,3,3,3,3,23581,3,3,3,3,3,23593,3,3,
23599,3,23603,3,3,23609,3,3,3,3,3,3,23623,3,23627,
23629,3,23633,3,3,3,3,3,3,3,3,3,3,3,3,3,3,23663,3,3,
23669,23671,3,3,23677,3,3,3,3,23687,23689,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,23719,3,3,3,3,3,3,3,3,3,3,23741,
23743,3,23747,3,3,23753,3,3,3,23761,3,3,23767,3,3,
23773,3,3,3,3,3,3,3,23789,3,3,3,3,3,23801,3,3,3,3,3,
23813,3,3,23819,3,3,3,23827,3,23831,23833,3,3,3,3,3,
3,3,3,3,3,3,23857,3,3,3,3,3,23869,3,23873,3,3,23879,
3,3,3,23887,3,3,23893,3,3,23899,3,3,3,3,23909,23911,
3,3,23917,3,3,3,3,3,23929,3,3,3,3,3,3,3,3,3,3,3,3,3,
23957,3,3,3,3,3,3,23971,3,3,23977,3,23981,3,3,3,3,3,
23993,3,3,3,24001,3,3,24007,3,3,3,3,3,24019,3,24023,
3,3,24029,3,3,3,3,3,3,24043,3,3,24049,3,3,3,3,3,
24061,3,3,3,3,24071,3,3,24077,3,3,24083,3,3,3,24091,
3,3,24097,3,3,24103,3,24107,24109,3,24113,3,3,3,
24121,3,3,3,3,3,24133,3,24137,3,3,3,3,3,3,24151,3,3,
3,3,3,3,3,3,24169,3,3,3,3,24179,24181,3,3,3,3,3,3,3,
24197,3,3,24203,3,3,3,3,3,3,3,3,3,24223,3,3,24229,3,
3,3,3,24239,3,3,3,24247,3,24251,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,24281,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,24317,3,3,
3,3,3,24329,3,3,3,24337,3,3,3,3,3,3,3,3,3,3,24359,3,3,
3,3,3,24371,24373,3,3,24379,3,3,3,3,3,24391,3,3,3,3,
3,3,3,24407,3,3,24413,3,3,24419,24421,3,3,3,3,3,3,3,
3,24439,3,24443,3,3,3,3,3,3,3,3,3,3,3,3,24469,3,
24473,3,3,3,24481,3,3,3,3,3,3,3,3,24499,3,3,3,3,
24509,3,3,3,24517,3,3,3,3,24527,3,3,24533,3,3,3,3,3,
3,24547,3,24551,3,3,3,3,3,3,3,3,3,24571,3,3,3,3,3,3,3,
3,3,3,24593,3,3,3,3,3,3,3,3,24611,3,3,3,3,3,24623,3,3,
3,24631,3,3,3,3,3,3,3,3,3,3,3,3,3,24659,3,3,3,3,3,
24671,3,3,24677,3,3,24683,3,3,3,24691,3,3,24697,3,3,
3,3,3,24709,3,3,3,3,3,3,3,3,3,3,3,24733,3,3,3,3,3,3,3,
24749,3,3,3,3,3,3,24763,3,24767,3,3,3,3,3,3,24781,3,
3,3,3,3,24793,3,3,24799,3,3,3,3,24809,3,3,3,3,3,
24821,3,3,3,3,3,3,3,3,3,24841,3,3,24847,3,24851,3,3,
3,24859,3,3,3,3,3,3,3,3,24877,3,3,3,3,3,24889,3,3,3,3,
3,3,3,3,24907,3,3,3,3,24917,24919,3,24923,3,3,3,3,3,
3,3,3,3,24943,3,3,3,3,24953,3,3,3,3,3,3,24967,3,
24971,3,3,24977,24979,3,3,3,3,24989,3,3,3,3,3,3,3,3,
3,3,3,25013,3,3,3,3,3,3,3,3,25031,25033,3,25037,3,3,
3,3,3,3,3,3,3,25057,3,3,3,3,3,3,3,25073,3,3,3,3,3,3,
25087,3,3,3,3,25097,3,3,3,3,3,3,25111,3,3,25117,3,
25121,3,3,25127,3,3,3,3,3,3,3,3,3,25147,3,3,25153,3,
3,3,3,25163,3,3,25169,25171,3,3,3,3,3,25183,3,3,
25189,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25219,3,3,3,3,25229,
3,3,3,25237,3,3,25243,3,25247,3,3,25253,3,3,3,25261,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25301,25303,3,
25307,25309,3,3,3,3,3,25321,3,3,3,3,3,3,3,3,25339,3,
25343,3,3,25349,3,3,3,25357,3,3,3,3,25367,3,3,
25373,3,3,3,3,3,3,3,3,25391,3,3,3,3,3,3,3,3,25409,
25411,3,3,3,3,3,25423,3,3,3,3,3,3,3,25439,3,3,3,25447,
3,3,25453,3,25457,3,3,25463,3,3,25469,25471,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,25523,3,3,3,3,3,
3,25537,3,25541,3,3,3,3,3,3,3,3,3,25561,3,3,3,3,3,3,3,
25577,25579,3,25583,3,3,25589,3,3,3,3,3,25601,
25603,3,3,25609,3,3,3,3,3,25621,3,3,3,3,3,25633,3,3,
25639,3,25643,3,3,3,3,3,3,25657,3,3,3,3,25667,3,3,
25673,3,3,25679,3,3,3,3,3,3,25693,3,3,3,3,25703,3,3,
3,3,3,3,25717,3,3,3,3,3,3,3,25733,3,3,3,25741,3,3,
25747,3,3,3,3,3,25759,3,25763,3,3,3,25771,3,3,3,3,3,
3,3,3,3,3,25793,3,3,25799,25801,3,3,3,3,3,3,3,3,
25819,3,3,3,3,3,3,3,3,3,3,25841,3,3,25847,25849,3,3,
3,3,3,3,3,3,25867,3,3,25873,3,3,3,3,3,3,3,25889,3,3,3,
3,3,3,25903,3,3,3,3,25913,3,3,25919,3,3,3,3,3,25931,
25933,3,3,25939,3,25943,3,3,3,25951,3,3,3,3,3,3,3,3,
25969,3,3,3,3,3,25981,3,3,3,3,3,3,3,25997,25999,3,
26003,3,3,3,3,3,3,26017,3,26021,3,3,3,26029,3,3,3,3,
3,26041,3,3,3,3,3,26053,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
26083,3,3,3,3,3,3,3,26099,3,3,3,26107,3,26111,26113,
3,3,26119,3,3,3,3,3,3,3,3,3,3,26141,3,3,3,3,3,26153,3,
3,3,26161,3,3,3,3,26171,3,3,26177,3,3,26183,3,3,
26189,3,3,3,3,3,3,26203,3,3,26209,3,3,3,3,3,3,3,3,
26227,3,3,3,3,26237,3,3,3,3,3,26249,26251,3,3,3,3,
26261,26263,3,26267,3,3,3,3,3,3,3,3,3,3,3,3,26293,3,
26297,3,3,3,3,3,26309,3,3,3,26317,3,26321,3,3,3,3,3,
3,3,3,26339,3,3,3,26347,3,3,3,3,26357,3,3,3,3,3,3,
26371,3,3,3,3,3,3,3,26387,3,3,26393,3,3,26399,3,3,3,
26407,3,3,3,3,26417,3,3,26423,3,3,3,26431,3,3,26437,
3,3,3,3,3,26449,3,3,3,3,26459,3,3,3,3,3,3,3,3,3,26479,
3,3,3,3,26489,3,3,3,26497,3,26501,3,3,3,3,3,26513,3,
3,3,3,3,3,3,3,3,3,3,3,26539,3,3,3,3,3,3,3,3,26557,3,
26561,3,3,3,3,3,26573,3,3,3,3,3,3,3,3,26591,3,3,
26597,3,3,3,3,3,3,3,3,3,3,3,3,3,3,26627,3,3,26633,3,3,
3,26641,3,3,26647,3,3,3,3,3,3,3,3,3,3,26669,3,3,3,3,3,
26681,26683,3,26687,3,3,26693,3,3,26699,26701,3,3,
3,3,26711,26713,3,26717,3,3,26723,3,3,26729,26731,
3,3,26737,3,3,3,3,3,3,3,3,3,3,26759,3,3,3,3,3,3,3,3,
26777,3,3,26783,3,3,3,3,3,3,3,3,26801,3,3,3,3,3,
26813,3,3,3,26821,3,3,3,3,3,26833,3,3,26839,3,3,3,3,
26849,3,3,3,3,3,26861,26863,3,3,3,3,3,3,3,26879,
26881,3,3,3,3,26891,26893,3,3,3,3,26903,3,3,3,3,3,3,
3,3,26921,3,3,26927,3,3,3,3,3,3,3,3,3,26947,3,26951,
26953,3,3,26959,3,3,3,3,3,3,3,3,3,3,26981,3,3,26987,
3,3,26993,3,3,3,3,3,3,3,3,27011,3,3,27017,3,3,3,3,3,3,
27031,3,3,3,3,3,27043,3,3,3,3,3,3,3,27059,27061,3,3,
27067,3,3,27073,3,27077,3,3,3,3,3,3,27091,3,3,3,3,3,
27103,3,27107,27109,3,3,3,3,3,3,3,3,27127,3,3,3,3,3,
3,3,27143,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27179,3,3,3,
3,3,27191,3,3,27197,3,3,3,3,3,3,27211,3,3,3,3,3,3,3,3,
3,3,3,3,3,27239,27241,3,3,3,3,3,27253,3,3,27259,3,3,
3,3,3,27271,3,3,27277,3,27281,27283,3,3,3,3,3,3,3,
27299,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27329,3,3,3,27337,3,
3,3,3,3,3,3,3,3,3,3,27361,3,3,27367,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,27397,3,3,3,3,27407,27409,3,3,3,3,3,3,3,3,
27427,3,27431,3,3,27437,3,3,3,3,3,27449,3,3,3,27457,
3,3,3,3,3,3,3,3,3,3,27479,27481,3,3,27487,3,3,3,3,3,3,
3,3,3,3,27509,3,3,3,3,3,3,3,3,27527,27529,3,3,3,3,
27539,27541,3,3,3,3,27551,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
27581,27583,3,3,3,3,3,3,3,3,3,3,3,3,3,27611,3,3,27617,
3,3,3,3,3,3,27631,3,3,3,3,3,3,3,27647,3,3,27653,3,3,3,
3,3,3,3,3,3,27673,3,3,3,3,3,3,3,27689,27691,3,3,
27697,3,27701,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,27733,3,
27737,27739,3,27743,3,3,27749,27751,3,3,3,3,3,
27763,3,27767,3,3,27773,3,3,27779,3,3,3,3,3,27791,
27793,3,3,27799,3,27803,3,3,27809,3,3,3,27817,3,3,
27823,3,27827,3,3,3,3,3,3,3,3,3,27847,3,27851,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,27883,3,3,3,3,27893,3,3,3,
27901,3,3,3,3,3,3,3,27917,27919,3,3,3,3,3,3,3,3,3,3,
27941,27943,3,27947,3,3,27953,3,3,3,27961,3,3,
27967,3,3,3,3,3,3,3,27983,3,3,3,3,3,3,27997,3,28001,
3,3,3,3,3,3,3,3,28019,3,3,3,28027,3,28031,3,3,3,3,3,3,
3,3,3,28051,3,3,28057,3,3,3,3,3,28069,3,3,3,3,3,
28081,3,3,28087,3,3,3,3,28097,28099,3,3,3,3,28109,
28111,3,3,3,3,3,28123,3,3,3,3,3,3,3,3,3,3,3,3,3,28151,
3,3,3,3,3,28163,3,3,3,3,3,3,3,3,28181,28183,3,3,3,3,3,
3,3,3,28201,3,3,3,3,28211,3,3,3,28219,3,3,3,3,28229,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28277,28279,
3,28283,3,3,28289,3,3,3,28297,3,3,3,3,28307,28309,3,
3,3,3,28319,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28349,28351,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,28387,3,3,28393,3,3,3,3,
28403,3,3,28409,28411,3,3,3,3,3,3,3,3,28429,3,28433,
3,3,28439,3,3,3,28447,3,3,3,3,3,3,3,28463,3,3,3,3,3,3,
28477,3,3,3,3,3,3,3,28493,3,3,28499,3,3,3,3,3,3,
28513,3,28517,3,3,3,3,3,3,3,3,3,28537,3,28541,3,3,
28547,28549,3,3,3,3,28559,3,3,3,3,3,28571,28573,3,3,
28579,3,3,3,3,3,28591,3,3,28597,3,3,28603,3,28607,3,
3,3,3,3,28619,28621,3,3,28627,3,28631,3,3,3,3,3,
28643,3,3,28649,3,3,3,28657,3,28661,28663,3,3,
28669,3,3,3,3,3,3,3,3,28687,3,3,3,3,28697,3,3,28703,
3,3,3,28711,3,3,3,3,3,28723,3,3,28729,3,3,3,3,3,3,3,3,
3,3,28751,28753,3,3,28759,3,3,3,3,3,28771,3,3,3,3,3,
3,3,3,28789,3,28793,3,3,3,3,3,3,28807,3,3,28813,3,
28817,3,3,3,3,3,3,3,3,3,28837,3,3,28843,3,3,3,3,3,3,3,
28859,3,3,3,28867,3,28871,3,3,3,28879,3,3,3,3,3,3,3,
3,3,3,28901,3,3,3,28909,3,3,3,3,3,28921,3,3,28927,3,
3,28933,3,3,3,3,3,3,3,28949,3,3,3,3,3,28961,3,3,3,3,3,
3,3,3,28979,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29009,3,3,3,
29017,3,29021,29023,3,29027,3,3,29033,3,3,3,3,3,3,3,
3,3,3,3,3,29059,3,29063,3,3,3,3,3,3,29077,3,3,3,3,3,3,
3,3,3,3,3,29101,3,3,3,3,3,3,3,3,3,3,29123,3,3,29129,
29131,3,3,29137,3,3,3,3,29147,3,3,29153,3,3,3,3,3,3,
29167,3,3,29173,3,3,29179,3,3,3,3,3,29191,3,3,3,3,
29201,3,3,29207,29209,3,3,3,3,3,29221,3,3,3,3,29231,
3,3,3,3,3,29243,3,3,3,29251,3,3,3,3,3,3,3,3,29269,3,3,
3,3,3,3,3,3,29287,3,3,3,3,29297,3,3,29303,3,3,3,29311,
3,3,3,3,3,3,3,29327,3,3,29333,3,3,29339,3,3,3,29347,
3,3,3,3,3,3,3,29363,3,3,3,3,3,3,3,3,3,29383,3,29387,
29389,3,3,3,3,29399,29401,3,3,3,3,29411,3,3,3,3,3,
29423,3,3,29429,3,3,3,29437,3,3,29443,3,3,3,3,29453,
3,3,3,3,3,3,3,3,3,29473,3,3,3,3,29483,3,3,3,3,3,3,3,3,
29501,3,3,3,3,3,3,3,3,3,3,3,3,29527,3,29531,3,3,
29537,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29567,29569,3,
29573,3,3,3,29581,3,3,29587,3,3,3,3,3,29599,3,3,3,3,
3,29611,3,3,3,3,3,3,3,3,29629,3,29633,3,3,3,29641,3,3,
3,3,3,3,3,3,3,3,29663,3,3,29669,29671,3,3,3,3,3,
29683,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,29717,3,3,29723,
3,3,3,3,3,3,3,3,29741,3,3,3,3,3,29753,3,3,29759,
29761,3,3,3,3,3,3,3,3,3,3,3,3,3,29789,3,3,3,3,3,3,
29803,3,3,3,3,3,3,3,29819,3,3,3,3,3,3,29833,3,29837,
3,3,3,3,3,3,29851,3,3,3,3,3,29863,3,29867,3,3,29873,
3,3,29879,29881,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
29917,3,29921,3,3,29927,3,3,3,3,3,3,3,3,3,29947,3,3,
3,3,3,29959,3,3,3,3,3,3,3,3,3,3,3,29983,3,3,29989,3,3,
3,3,3,3,3,3,3,3,30011,30013,3,3,3,3,3,3,3,30029,3,3,3,
3,3,3,3,3,30047,3,3,3,3,3,30059,3,3,3,3,3,30071,3,3,3,
3,3,3,3,3,30089,30091,3,3,30097,3,3,30103,3,3,30109,
3,30113,3,3,30119,3,3,3,3,3,3,30133,3,30137,30139,3,
3,3,3,3,3,3,3,3,3,30161,3,3,3,30169,3,3,3,3,3,30181,3,
3,30187,3,3,3,3,30197,3,3,30203,3,3,3,30211,3,3,3,3,3,
30223,3,3,3,3,3,3,3,3,30241,3,3,3,3,3,30253,3,3,
30259,3,3,3,3,30269,30271,3,3,3,3,3,3,3,3,3,3,30293,
3,3,3,3,3,3,30307,3,3,30313,3,3,30319,3,30323,3,3,3,
3,3,3,3,3,30341,3,3,30347,3,3,3,3,3,3,3,3,3,30367,3,3,
3,3,3,3,3,3,3,3,30389,30391,3,3,3,3,3,30403,3,3,3,3,3,
3,3,3,3,3,3,30427,3,30431,3,3,3,3,3,3,3,3,30449,3,3,3,
3,3,3,3,3,30467,30469,3,3,3,3,3,3,3,3,3,3,30491,
30493,3,30497,3,3,3,3,3,30509,3,3,3,30517,3,3,3,3,3,
30529,3,3,3,3,30539,3,3,3,3,3,3,30553,3,30557,30559,
3,3,3,3,3,3,3,3,30577,3,3,3,3,3,3,3,30593,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,30631,3,3,30637,3,3,30643,3,3,
30649,3,3,3,3,3,30661,3,3,3,3,30671,3,3,30677,3,3,3,
3,3,30689,3,3,3,30697,3,3,30703,3,30707,3,3,30713,3,
3,3,3,3,3,30727,3,3,3,3,3,3,3,3,3,3,3,3,3,3,30757,3,3,
30763,3,3,3,3,30773,3,3,3,30781,3,3,3,3,3,3,3,3,3,3,
30803,3,3,30809,3,3,3,30817,3,3,3,3,3,30829,3,3,3,3,
30839,30841,3,3,3,3,30851,30853,3,3,30859,3,3,3,3,
30869,30871,3,3,3,3,30881,3,3,3,3,3,30893,3,3,3,3,3,
3,3,3,30911,3,3,3,3,3,3,3,3,3,30931,3,3,30937,3,30941,
3,3,3,30949,3,3,3,3,3,3,3,3,3,3,30971,3,3,30977,3,3,
30983,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31013,3,3,31019,3,3,
3,3,3,3,31033,3,3,31039,3,3,3,3,3,31051,3,3,3,3,3,
31063,3,3,31069,3,3,3,3,31079,31081,3,3,3,3,31091,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,31121,31123,3,3,3,3,3,3,3,
31139,3,3,3,31147,3,31151,31153,3,3,31159,3,3,3,3,3,
3,3,3,31177,3,31181,31183,3,3,31189,3,31193,3,3,3,3,
3,3,3,3,3,3,3,3,31219,3,31223,3,3,3,31231,3,3,31237,
3,3,3,3,31247,31249,3,31253,3,3,31259,3,3,3,31267,3,
31271,3,3,31277,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31307,3,3,
3,3,3,31319,31321,3,3,31327,3,3,31333,3,31337,3,3,3,
3,3,3,3,3,3,31357,3,3,3,3,3,3,3,3,3,3,31379,3,3,3,
31387,3,31391,31393,3,31397,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31469,3,3,3,
31477,3,31481,3,3,3,31489,3,3,3,3,3,3,3,3,3,3,31511,
31513,3,31517,3,3,3,3,3,3,31531,3,3,3,3,31541,31543,
3,31547,3,3,3,3,3,3,3,3,3,31567,3,3,31573,3,3,3,3,
31583,3,3,3,3,3,3,3,3,31601,3,3,31607,3,3,3,3,3,3,3,3,
3,31627,3,3,3,3,3,3,3,31643,3,3,31649,3,3,3,31657,3,
3,31663,3,31667,3,3,3,3,3,3,3,3,3,31687,3,3,3,3,3,
31699,3,3,3,3,3,3,3,3,3,3,31721,31723,3,31727,31729,
3,3,3,3,3,31741,3,3,3,3,31751,3,3,3,3,3,3,3,3,31769,
31771,3,3,3,3,3,3,3,3,3,3,31793,3,3,31799,3,3,3,3,3,3,
3,3,31817,3,3,3,3,3,3,3,3,3,3,3,3,3,3,31847,31849,3,3,
3,3,31859,3,3,3,3,3,3,31873,3,3,3,3,31883,3,3,3,
31891,3,3,3,3,3,3,3,31907,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,31957,3,3,31963,3,3,3,3,31973,3,3,3,
31981,3,3,3,3,31991,3,3,3,3,3,32003,3,3,32009,3,3,3,
3,3,3,3,3,32027,32029,3,3,3,3,3,3,3,3,3,3,32051,3,3,
32057,32059,3,32063,3,3,32069,3,3,3,32077,3,3,
32083,3,3,32089,3,3,3,3,32099,3,3,3,3,3,3,3,3,32117,
32119,3,3,3,3,3,3,3,3,3,3,32141,32143,3,3,3,3,3,3,3,
32159,3,3,3,3,3,3,32173,3,3,3,3,32183,3,3,32189,
32191,3,3,3,3,3,32203,3,3,3,3,32213,3,3,3,3,3,3,3,3,3,
32233,3,32237,3,3,3,3,3,3,32251,3,3,32257,3,32261,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,32297,32299,3,32303,3,
3,32309,3,3,3,3,3,32321,32323,3,32327,3,3,3,3,3,3,
32341,3,3,3,3,3,32353,3,3,32359,3,32363,3,3,32369,
32371,3,3,32377,3,32381,3,3,3,3,3,3,3,3,3,32401,3,3,
3,3,32411,32413,3,3,3,3,32423,3,3,32429,3,3,3,3,3,
32441,32443,3,3,3,3,3,3,3,3,3,3,3,32467,3,3,3,3,3,
32479,3,3,3,3,3,32491,3,3,32497,3,3,32503,3,32507,3,
3,3,3,3,3,3,3,3,3,3,32531,32533,3,32537,3,3,3,3,3,3,3,
3,3,3,3,32561,32563,3,3,32569,3,32573,3,3,32579,3,3,
3,32587,3,3,3,3,3,3,3,32603,3,3,32609,32611,3,3,3,3,
32621,3,3,3,3,3,32633,3,3,3,3,3,3,32647,3,3,32653,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,32687,3,3,32693,3,3,3,3,3,
3,32707,3,3,32713,3,32717,32719,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,32749,3,3,3,3,3,3,3,3,3,3,32771,3,3,3,32779,3,
32783,3,3,32789,3,3,3,32797,3,32801,32803,3,3,3,3,3,
3,3,3,3,3,3,3,3,32831,32833,3,3,32839,3,32843,3,3,3,
3,3,3,3,3,3,3,3,3,32869,3,3,3,3,3,3,3,3,32887,3,3,3,3,3,
3,3,3,3,3,32909,32911,3,3,32917,3,3,3,3,3,3,3,32933,3,
3,32939,32941,3,3,3,3,3,3,3,32957,3,3,3,3,3,32969,
32971,3,3,3,3,3,32983,3,32987,3,3,32993,3,3,32999,3,
3,3,3,3,3,33013,3,3,3,3,33023,3,3,33029,3,3,3,33037,
3,3,3,3,3,33049,3,33053,3,3,3,3,3,3,3,3,33071,33073,
3,3,3,3,33083,3,3,3,33091,3,3,3,3,3,3,3,33107,3,3,
33113,3,3,33119,3,3,3,3,3,3,3,3,3,3,3,3,3,3,33149,
33151,3,3,3,3,33161,3,3,3,3,3,3,3,3,33179,33181,3,3,
3,3,33191,3,3,3,33199,3,33203,3,3,3,33211,3,3,3,3,3,
33223,3,3,3,3,3,3,3,3,3,3,3,33247,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,33287,33289,3,3,3,3,3,33301,3,3,3,3,
33311,3,3,33317,3,3,3,3,3,33329,33331,3,3,3,3,3,
33343,3,33347,33349,3,33353,3,3,33359,3,3,3,3,3,3,3,
3,33377,3,3,3,3,3,3,33391,3,3,3,3,3,33403,3,3,33409,
3,33413,3,3,3,3,3,3,33427,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
33457,3,33461,3,3,3,33469,3,3,3,3,33479,3,3,3,33487,
3,3,33493,3,3,3,3,33503,3,3,3,3,3,3,3,3,33521,3,3,3,
33529,3,33533,3,3,3,3,3,3,33547,3,3,3,3,3,3,3,33563,
3,3,33569,3,3,3,33577,3,33581,3,3,33587,33589,3,3,3,
3,33599,33601,3,3,3,3,3,33613,3,33617,33619,3,
33623,3,3,33629,3,3,3,33637,3,33641,3,3,33647,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,33679,3,3,3,3,3,3,3,3,3,3,3,
33703,3,3,3,3,33713,3,3,3,33721,3,3,3,3,3,3,3,3,
33739,3,3,3,3,33749,33751,3,3,33757,3,3,3,3,33767,
33769,3,33773,3,3,3,3,3,3,3,3,33791,3,3,33797,3,3,3,
3,3,33809,33811,3,3,3,3,3,3,3,33827,33829,3,3,3,3,3,3,
3,3,3,3,33851,3,3,33857,3,3,33863,3,3,3,33871,3,3,3,
3,3,3,3,3,33889,3,33893,3,3,3,3,3,3,3,3,33911,3,3,3,3,
3,33923,3,3,3,33931,3,3,33937,3,33941,3,3,3,3,3,3,3,
3,3,33961,3,3,33967,3,3,3,3,3,3,3,3,3,3,3,3,3,3,33997,
3,3,3,3,3,3,3,3,3,3,34019,3,3,3,3,3,34031,34033,3,3,
34039,3,3,3,3,3,3,3,3,34057,3,34061,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,34123,3,34127,
34129,3,3,3,3,3,34141,3,3,34147,3,3,3,3,34157,34159,
3,3,3,3,3,34171,3,3,3,3,3,34183,3,3,3,3,3,3,3,3,3,3,3,3,
3,34211,34213,3,34217,3,3,3,3,3,3,34231,3,3,3,3,3,3,3,
3,3,3,34253,3,3,34259,34261,3,3,34267,3,3,34273,3,3,
3,3,34283,3,3,3,3,3,3,34297,3,34301,34303,3,3,3,3,
34313,3,3,34319,3,3,3,34327,3,3,3,3,34337,3,3,3,3,3,
3,34351,3,3,3,3,34361,3,3,34367,34369,3,3,3,3,3,
34381,3,3,3,3,3,3,3,3,3,3,34403,3,3,3,3,3,3,3,3,34421,
3,3,3,34429,3,3,3,3,34439,3,3,3,3,3,3,3,3,34457,3,3,3,
3,3,34469,34471,3,3,3,3,3,34483,3,34487,3,3,3,3,3,
34499,34501,3,3,3,3,34511,34513,3,3,34519,3,3,3,3,3,
3,3,3,34537,3,3,34543,3,3,34549,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,34583,3,3,34589,34591,3,3,3,3,3,34603,3,
34607,3,3,34613,3,3,3,3,3,3,3,3,34631,3,3,3,3,3,3,3,3,
34649,34651,3,3,3,3,3,3,3,34667,3,3,34673,3,3,34679,
3,3,3,34687,3,3,34693,3,3,3,3,34703,3,3,3,3,3,3,3,3,
34721,3,3,3,34729,3,3,3,3,34739,3,3,3,34747,3,3,3,3,
34757,34759,3,34763,3,3,3,3,3,3,3,3,34781,3,3,3,3,3,
3,3,3,3,3,3,3,34807,3,3,3,3,3,34819,3,3,3,3,3,3,3,3,3,3,
34841,34843,3,34847,34849,3,3,3,3,3,3,3,3,3,3,34871,
3,3,34877,3,3,34883,3,3,3,3,3,3,34897,3,3,3,3,3,3,3,
34913,3,3,34919,3,3,3,3,3,3,3,3,3,34939,3,3,3,3,
34949,3,3,3,3,3,34961,34963,3,3,3,3,3,3,3,3,34981,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,35023,3,35027,3,3,
3,3,3,3,3,3,3,3,3,35051,35053,3,3,35059,3,3,3,3,
35069,3,3,3,3,3,35081,35083,3,3,35089,3,3,3,3,35099,
3,3,3,35107,3,35111,3,3,35117,3,3,3,3,3,35129,3,3,3,3,
3,35141,3,3,3,35149,3,35153,3,3,35159,3,3,3,3,3,
35171,3,3,3,3,3,3,3,3,3,3,3,3,3,3,35201,3,3,3,3,3,3,3,3,
3,35221,3,3,35227,3,3,3,3,3,3,3,3,3,3,3,35251,3,3,
35257,3,3,3,3,35267,3,3,3,3,3,35279,35281,3,3,3,3,
35291,3,3,3,3,3,3,3,3,3,35311,3,3,35317,3,3,35323,3,
35327,3,3,3,3,3,35339,3,3,3,3,3,3,35353,3,3,3,3,
35363,3,3,3,3,3,3,3,3,35381,3,3,3,3,3,35393,3,3,3,
35401,3,3,35407,3,3,3,3,3,35419,3,35423,3,3,3,3,3,3,
35437,3,3,3,3,35447,35449,3,3,3,3,3,35461,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,35491,3,3,3,3,3,3,3,35507,35509,3,3,
3,3,3,35521,3,3,35527,3,35531,35533,3,35537,3,3,
35543,3,3,3,3,3,3,3,3,3,3,3,3,35569,3,35573,3,3,3,3,3,
3,3,3,35591,35593,3,35597,3,3,35603,3,3,3,3,3,3,
35617,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
35671,3,3,35677,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,35729,35731,3,3,3,3,3,3,3,35747,3,3,35753,
3,3,35759,3,3,3,3,3,35771,3,3,3,3,3,3,3,3,3,3,3,3,
35797,3,35801,35803,3,3,35809,3,3,3,3,3,3,3,3,3,3,
35831,3,3,35837,35839,3,3,3,3,3,35851,3,3,3,3,3,
35863,3,3,35869,3,3,3,3,35879,3,3,3,3,3,3,3,3,35897,
35899,3,3,3,3,3,35911,3,3,3,3,3,35923,3,3,3,3,35933,3,
3,3,3,3,3,3,3,35951,3,3,3,3,3,35963,3,3,35969,3,3,3,
35977,3,3,35983,3,3,3,3,35993,3,3,35999,3,3,3,36007,
3,36011,36013,3,36017,3,3,3,3,3,3,3,3,3,36037,3,3,3,3,
3,3,3,3,3,3,3,36061,3,3,36067,3,3,36073,3,3,3,3,
36083,3,3,3,3,3,3,36097,3,3,3,3,36107,36109,3,3,3,3,
3,3,3,3,3,3,36131,3,3,36137,3,3,3,3,3,3,36151,3,3,3,3,
36161,3,3,3,3,3,3,3,3,3,3,3,3,36187,3,36191,3,3,3,3,3,
3,3,3,36209,3,3,3,36217,3,3,3,3,3,36229,3,3,3,3,3,
36241,3,3,3,3,36251,3,3,3,3,3,36263,3,3,36269,3,3,3,
36277,3,3,3,3,3,3,3,36293,3,3,36299,3,3,3,36307,3,3,
36313,3,3,36319,3,3,3,3,3,3,3,3,3,3,36341,36343,3,3,
3,3,36353,3,3,3,3,3,3,3,3,3,36373,3,3,3,3,36383,3,3,
36389,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,36433,3,
3,3,3,3,3,3,3,36451,3,3,36457,3,3,3,3,36467,36469,3,
36473,3,3,36479,3,3,3,3,3,3,36493,3,36497,3,3,3,3,3,
3,3,3,3,3,3,3,36523,3,36527,36529,3,3,3,3,3,36541,3,
3,3,3,36551,3,3,3,36559,3,36563,3,3,3,36571,3,3,3,3,
3,36583,3,36587,3,3,3,3,3,36599,3,3,3,36607,3,3,3,3,
3,3,3,3,3,3,36629,3,3,3,36637,3,3,36643,3,3,3,3,
36653,3,3,3,3,3,3,3,3,36671,3,3,36677,3,3,36683,3,3,
3,36691,3,3,36697,3,3,3,3,3,36709,3,36713,3,3,3,
36721,3,3,3,3,3,3,3,3,36739,3,3,3,3,36749,3,3,3,3,3,
36761,3,3,36767,3,3,3,3,3,36779,36781,3,3,36787,3,
36791,36793,3,3,3,3,3,3,3,36809,3,3,3,3,3,36821,3,3,
3,3,3,36833,3,3,3,3,3,3,36847,3,3,3,3,36857,3,3,3,3,3,
3,36871,3,3,36877,3,3,3,3,36887,3,3,3,3,3,36899,
36901,3,3,3,3,3,36913,3,3,36919,3,36923,3,3,36929,
36931,3,3,3,3,3,36943,3,36947,3,3,3,3,3,3,3,3,3,3,3,3,
36973,3,3,36979,3,3,3,3,3,3,3,3,36997,3,3,37003,3,3,
3,3,37013,3,3,37019,37021,3,3,3,3,3,3,3,3,37039,3,3,
3,3,37049,3,3,3,37057,3,37061,3,3,3,3,3,3,3,3,3,3,3,3,
37087,3,3,3,3,37097,3,3,3,3,3,3,3,3,3,37117,3,3,37123,
3,3,3,3,3,3,3,37139,3,3,3,3,3,3,3,3,3,37159,3,3,3,3,3,
37171,3,3,3,3,37181,3,3,3,37189,3,3,3,3,37199,37201,
3,3,3,3,3,3,3,37217,3,3,37223,3,3,3,3,3,3,3,3,3,37243,
3,3,3,3,37253,3,3,3,3,3,3,3,3,3,37273,3,37277,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,37307,37309,3,37313,3,3,3,37321,
3,3,3,3,3,3,3,37337,37339,3,3,3,3,3,3,3,3,37357,3,
37361,37363,3,3,37369,3,3,3,3,37379,3,3,3,3,3,3,3,3,
37397,3,3,3,3,3,37409,3,3,3,3,3,3,37423,3,3,3,3,3,3,3,
3,37441,3,3,37447,3,3,3,3,3,3,3,37463,3,3,3,3,3,3,3,3,
3,37483,3,3,37489,3,37493,3,3,3,37501,3,3,37507,3,
37511,3,3,37517,3,3,3,3,3,37529,3,3,3,37537,3,3,3,3,
37547,37549,3,3,3,3,3,37561,3,3,37567,3,37571,
37573,3,3,37579,3,3,3,3,37589,37591,3,3,3,3,3,3,3,
37607,3,3,3,3,3,37619,3,3,3,3,3,3,37633,3,3,3,3,
37643,3,3,37649,3,3,3,37657,3,3,37663,3,3,3,3,3,3,3,
3,3,3,3,3,3,37691,37693,3,3,37699,3,3,3,3,3,3,3,3,
37717,3,3,3,3,3,3,3,3,3,3,3,3,3,3,37747,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,37781,37783,3,3,3,3,3,3,3,37799,3,3,3,
3,3,37811,37813,3,3,3,3,3,3,3,3,37831,3,3,3,3,3,3,3,
37847,3,3,37853,3,3,3,37861,3,3,3,3,37871,3,3,3,
37879,3,3,3,3,37889,3,3,3,37897,3,3,3,3,37907,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,37951,3,3,37957,3,3,
37963,3,37967,3,3,3,3,3,3,3,3,3,37987,3,37991,37993,
3,37997,3,3,3,3,3,3,38011,3,3,3,3,3,3,3,3,3,3,3,3,3,
38039,3,3,3,38047,3,3,38053,3,3,3,3,3,3,3,38069,3,3,
3,3,3,3,38083,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38113,3,3,
38119,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38149,3,38153,3,3,3,
3,3,3,38167,3,3,3,3,38177,3,3,38183,3,3,38189,3,3,3,
38197,3,38201,3,3,3,3,3,3,3,3,38219,3,3,3,3,3,38231,
3,3,38237,38239,3,3,3,3,3,3,3,3,3,3,38261,3,3,3,3,3,
38273,3,3,3,38281,3,3,38287,3,3,3,3,3,38299,3,38303,
3,3,3,3,3,3,38317,3,38321,3,3,38327,38329,3,38333,3,
3,3,3,3,3,3,3,38351,3,3,3,3,3,3,3,3,3,38371,3,3,38377,
3,3,3,3,3,3,3,38393,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
38431,3,3,3,3,3,3,3,38447,38449,3,38453,3,3,38459,
38461,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38501,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,38543,3,3,3,3,3,3,
38557,3,38561,3,3,38567,38569,3,3,3,3,3,3,3,3,3,3,3,
38593,3,3,3,3,38603,3,3,38609,38611,3,3,3,3,3,3,3,3,
38629,3,3,3,3,38639,3,3,3,3,3,38651,38653,3,3,3,3,3,
3,3,38669,38671,3,3,38677,3,3,3,3,3,3,3,38693,3,3,
38699,3,3,3,38707,3,38711,38713,3,3,3,3,38723,3,3,
38729,3,3,3,38737,3,3,3,3,38747,38749,3,3,3,3,3,3,3,
3,38767,3,3,3,3,3,3,3,38783,3,3,3,38791,3,3,3,3,3,
38803,3,3,3,3,3,3,3,3,38821,3,3,3,3,3,38833,3,3,
38839,3,3,3,3,3,38851,3,3,3,3,38861,3,3,38867,3,3,
38873,3,3,3,3,3,3,3,3,38891,3,3,3,3,3,38903,3,3,3,3,3,
3,38917,3,38921,38923,3,3,3,3,38933,3,3,3,3,3,3,3,3,
3,38953,3,3,38959,3,3,3,3,3,38971,3,3,38977,3,3,3,3,
3,3,3,38993,3,3,3,3,3,3,3,3,3,3,3,3,39019,3,39023,3,3,
3,3,3,3,3,3,39041,39043,3,39047,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,39079,3,3,3,3,39089,3,3,3,39097,3,3,39103,3,
39107,3,3,39113,3,3,39119,3,3,3,3,3,3,39133,3,3,
39139,3,3,3,3,3,3,3,3,39157,3,39161,39163,3,3,3,3,3,
3,3,3,39181,3,3,3,3,39191,3,3,3,39199,3,3,3,3,39209,
3,3,3,39217,3,3,3,3,39227,39229,3,39233,3,3,39239,
39241,3,3,3,3,39251,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,39293,3,3,3,39301,3,3,3,3,3,39313,3,39317,3,3,
39323,3,3,3,3,3,3,3,3,39341,39343,3,3,3,3,3,3,3,
39359,3,3,3,39367,3,39371,39373,3,3,3,3,39383,3,3,3,
3,3,3,39397,3,3,3,3,3,39409,3,3,3,3,39419,3,3,3,3,3,3,
3,3,3,39439,3,39443,3,3,3,39451,3,3,3,3,39461,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,39499,3,39503,3,3,39509,
39511,3,3,3,3,39521,3,3,3,3,3,3,3,3,3,39541,3,3,3,3,
39551,3,3,3,3,3,39563,3,3,39569,3,3,3,3,3,39581,3,3,
3,3,3,3,3,3,3,3,3,3,39607,3,3,3,3,3,39619,3,39623,3,3,
3,39631,3,3,3,3,3,3,3,3,3,3,3,3,3,39659,3,3,3,39667,3,
39671,3,3,3,39679,3,3,3,3,3,3,3,3,3,3,3,39703,3,3,
39709,3,3,3,3,39719,3,3,3,39727,3,3,39733,3,3,3,3,3,
3,3,39749,3,3,3,3,3,39761,3,3,3,39769,3,3,3,3,39779,
3,3,3,3,3,39791,3,3,3,39799,3,3,3,3,3,3,3,3,3,3,39821,
3,3,39827,39829,3,3,3,3,39839,39841,3,3,39847,3,3,3,
3,39857,3,3,39863,3,3,39869,3,3,3,39877,3,3,39883,3,
39887,3,3,3,3,3,3,39901,3,3,3,3,3,3,3,3,3,3,3,3,3,
39929,3,3,3,39937,3,3,3,3,3,3,3,39953,3,3,3,3,3,3,3,3,
39971,3,3,3,39979,3,39983,3,3,39989,3,3,3,3,3,3,3,3,
3,40009,3,40013,3,3,3,3,3,3,3,3,40031,3,3,40037,
40039,3,3,3,3,3,3,3,3,3,3,3,40063,3,3,3,3,3,3,3,3,3,3,3,
40087,3,3,40093,3,3,40099,3,3,3,3,3,40111,3,3,3,3,3,
40123,3,40127,40129,3,3,3,3,3,3,3,3,3,3,40151,40153,
3,3,3,3,40163,3,3,40169,3,3,3,40177,3,3,3,3,3,40189,
3,40193,3,3,3,3,3,3,3,3,3,40213,3,3,3,3,3,3,3,3,40231,
3,3,40237,3,40241,3,3,3,3,3,40253,3,3,3,3,3,3,3,3,3,3,
3,40277,3,3,40283,3,3,40289,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,3,40343,3,3,3,40351,3,3,40357,
3,40361,3,3,3,3,3,3,3,3,3,3,3,3,40387,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,40423,3,40427,40429,3,40433,3,3,3,3,
3,3,3,3,3,3,3,3,40459,3,3,3,3,3,40471,3,3,3,3,3,40483,
3,40487,3,3,40493,3,3,40499,3,3,3,40507,3,3,3,3,3,
40519,3,3,3,3,40529,40531,3,3,3,3,3,40543,3,3,3,3,3,
3,3,40559,3,3,3,3,3,3,3,3,40577,3,3,40583,3,3,3,
40591,3,3,40597,3,3,3,3,3,40609,3,3,3,3,3,3,3,3,
40627,3,3,3,3,40637,40639,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
3,3,3,3,3,3,3,3,3,3,3,3,40693,3,40697,40699,3,3,3,3,
40709,3,3,3,3,3,3,3,3,3,3,3,3,3,3,40739,3,3,3,3,3,
40751,3,3,3,40759,3,40763,3,3,3,40771,3,3,3,3,3,3,3,
40787,3,3,3,3,3,3,40801,3,3,3,3,3,40813,3,3,40819,3,
40823,3,3,40829,3,3,3,3,3,40841,3,3,40847,40849,3,
40853,3,3,3,3,3,3,40867,3,3,3,3,3,40879,3,40883,3,3,
3,3,3,3,40897,3,3,40903,3,3,3,3,3,3,3,3,3,3,3,40927,3,
3,40933,3,3,40939,3,3,3,3,40949,3,3,3,3,3,40961,3,3,
3,3,3,40973,3,3,3,3,3,3,3,3,3,40993,3,3,3,3,3,3,3,3,
41011,3,3,41017,3,3,41023,3,3,3,3,3,3,3,41039,3,3,3,
41047,3,41051,3,3,41057,3,3,3,3,3,3,3,3,3,41077,3,
41081,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,41113,3,41117,3,3,3,
3,3,3,41131,3,3,3,3,41141,41143,3,3,41149,3,3,3,3,3,
41161,3,3,3,3,3,3,3,41177,41179,3,41183,3,3,41189,3,
3,3,3,3,41201,41203,3,3
München, 17. Februar 2023
Gottfried Färberböck


